
Prehistory of Logic (principles of valid reasoning, inference, & demonstration) around 5,000 Years old
Evolution Of Science at least by 5,500 years ago
Valid reasoning has been employed in all periods of human history. However, logic studies the principles of valid reasoning, inference, and demonstration. It is probable that the idea of demonstrating a conclusion first arose in connection with geometry, which originally meant the same as “land measurement”. In particular, the ancient Egyptians had empirically discovered some truths of geometry, such as the formula for the volume of a truncated pyramid. The earliest recorded beginnings of geometry can be traced to early peoples, who discovered obtuse triangles in the ancient Indus Valley (see Harappan Mathematics), and ancient Babylonia (see Babylonian mathematics) from around 5,000 years ago. Early geometry was a collection of empirically discovered principles concerning lengths, angles, areas, and volumes, which were developed to meet some practical need in surveying, construction, astronomy, and various crafts. Among these were some surprisingly sophisticated principles, and a modern mathematician might be hard put to derive some of them without the use of calculus. Another origin can be seen in Babylonia. Esagil-kin-apli’s medical Diagnostic Handbook in the 2,11o years ago was based on a logical set of axioms and assumptions, while Babylonian astronomers in the 2,800 and 2,700 years ago employed an internal logic within their predictive planetary systems, an important contribution to the philosophy of science. So we have real-world origins such as sky observation in Babylonian astrology and land observation in Egyptian Geometry (from the Ancient Greek: geo- “earth”, -metron “measurement”). The field of astronomy, especially as it relates to mapping the positions of stars and planets on the celestial sphere and describing the relationship between movements of celestial bodies, served as an important source of geometric problems during the next one and a half millennia. In the classical world, both geometry and astronomy were considered to be part of the Quadrivium, a subset of the seven liberal arts considered essential for a free citizen to master. While the ancient Egyptians empirically discovered some truths of geometry, the great achievement of the ancient Greeks was to replace empirical methods by demonstrative science. The systematic study of this seems to have begun with the school of Pythagoras in the late sixth century BC. The three basic principles of geometry are as follows: Certain propositions must be accepted as true without demonstration; such a proposition is known as an axiom of geometry. Every proposition that is not an axiom of geometry must be demonstrated as follows from the axioms of geometry; such a demonstration is known as a proof or a “derivation” of the proposition. The proof must be formal; that is, the derivation of the proposition must be independent of the particular subject matter in question. Fragments of early proofs are preserved in the works of Plato and Aristotle.
Where do these laws of logic come from, to me?
If we want to get a causal explanation of the origin of logical laws (apart from positing them as fundamental to the universe), the proper way to understand their origin IS as derivative on rationality as developed by non-rational evolutionary means. Thus, in a way we could say laws of logic didn’t come from anywhere; these just are the rules of rationality as they can be articulated by explicitly rational beings. When rational beings came into existence by purely non-rational evolutionary processes, they came into being as following these rules. And then, at some later point in time they became aware of themselves following these rules, and able to represent them explicitly. When we see there as being implicitly logically-governed behavior in nature, we interpret nature in accordance with the way we understand ourselves as explicitly logical. We think of the behavior of entities of nature as if they represented their rational behavior like we do, it is our way of explicitly representing the norms of rationality. These non-rational entities of nature don’t have the slightest clue what the laws of logic are. But they behave as we do, and that’s how “we” see them. We can only make explanatory sense of how “we” have become explicitly aware of logical laws by showing how we are the result of beings that evolved an implicit awareness of these laws. And yet, we can only understand our natural ancestors as having an implicit grasp of logic once we’ve garnered an explicit grasp of logic. That’s the only way we can make sense of them as actually following the laws of logic. The reason it is unproblematic for an explanation to conceptually (but not causally) presuppose that laws of logic is that we cannot hope to get out of these laws conceptually, since they just are, the bounds of sense. When sense-makers like us naturally evolve this just is the way in which we must make sense of things. It’s is the essential structure of sense-making, so to speak. And since the explanation is a sense-making enterprise, and any coherent explanation will conform to sense’s bounds—the things we’ve come to describe as the laws of logic. ref, ref, ref, ref
Rationalism and the Enlightenment
Here is why “Reason is my only master”
The most Base Presupposition begins in reason. Reason is needed for logic (logic is realized by the aid of reason enriching its axioms). Logic is needed for axiology/value theory (axiology is realized by the aid of logic). Axiology is needed for epistemology (epistemology is realized by aid of axiology value judge and enrich its value assumptions as valid or not). Epistemology is needed for a good ontology (ontology is realized by the aid of epistemology justified assumptions/realizations/conclusions). Then when one possesses a good ontology (fortified with valid and reliable reason and evidence) they can then say they know the ontology of that thing. Thinking is good and one claiming otherwise is indeed a person erroring in reason. Which may I remind you is terrible since the most Base Presupposition in our understanding of everything begins in reason.
A General Thinking in all My Epistemology Theorizing is Justificationism
So, I think, right thinking is reason. Right reason is logic. Right logic, can be used for mathematics and from there we can get to science. And, by this methodological approach, we get one of the best ways of knowing the scientific method. Activating experience/event occurs, eliciting our feelings/scenes. Then naive thoughts occur, eliciting emotions as a response. Then it is our emotional intelligence over emotional hijacking, which entrance us but are unavoidable and that it is the navigating this successfully in a methodological way we call critical thinking or as In just call right thinking. So, to me, could be termed “Right” thinking, that is referring to a kind of methodological thinking. Reason is at the base of everything and it builds up from pragmatic approaches. And, to me, there are three main approaches to truth (ontology of truth) from the very subjective (Pragmatic theory of truth), to subjective (Coherence theory of truth), then onto objective (Correspondence theory of truth) but remember that this process as limited as it can be, is the best we have and we build one truth ontop another like blocks to a wall of truth.
Pragmatic theory of truth, Coherence theory of truth, and Correspondence theory of truth
Science and Justified True Beliefs
In a general way, all reality, in a philosophic sense, is an emergent property of reason, and knowing how reason accrues does not remove its warrant. Feelings are experienced then perceived, leading to thinking, right thinking is reason, right reason is logic, right logic is mathematics, right mathematics is physics and from there all science.
Science is quite the opposite of just common sense. To me, common sense is experience related interpretation, relatively, as it generally relates to the reality of things in the world, which involves “naive realism” as well as possible psychological certainty and low epistemic certainty. Whereas, most of those who are scientific thinkers, hold typically more to scientific realism or other stances far removed from the limited common sense of naive realism. Science is a multidisciplinary methodological quest for truth. Science understands what is, while religion is wishing on what is not. Scientific realism sees external reality as described by science is what is REAL and thus TRUE with the highest epistemic certainty regardless of possible psychological certainty.
Getting Real with Logic
On the Nature of Value (axiology)
Logic is the result of rationalism, as what do you think gets you to logic if not starting at reason? I want to hear your justification for your claims, all the presuppositions you are evading to explain the links in your claims of truth. As it is invalid to just claim this without a justification for your professed claims and the presupposing you do to get there, that is not trying to use rationalism to refuse rationalist thinking. How are you making the statement and not appearing to what is the rationale behind it? If not, you must want to think “Logic is self-generating as valid” and this understood value is to you not reducible to reason? You are devoid of an offer of your burden of proof, first just try to keep up with the thinker’s responsibility to provide more than unjustified claims. Logic is derived by axioms and thus using rationalism to validate them, think otherwise provide your proof. My Rationalism: is two things externalistic “scientific rationalism” a belief or theory that opinions and actions should be based on reason and knowledge rather than on religious belief or emotional response. And internalistic “philosophic rationalism” the theory that reason is the most base presupposition before all others, rather than simply trying to rely on experience is the foundation of certainty in knowledge. Activating experience occurs we then have thinking, right (methodological) thinking (critical thinking) is reason, right reason is logic, right logic can be used for math, right math in response to the natural world is physics, and from there all other Sciences, physics is the foundation for chemistry and chemistry is the foundation of biology. May reason be your only master and may you also master reason.
- Objective and Subjective Logic?
- Grasping the status of truth (ontology of truth): pre-logic, logic, and post-logic?
- Folk Logic: YOU CAN’T PROVE A NEGATIVE because you can PROVE A NEGATIVE
- Agnosticism Beliefs Involve “FOLK LOGIC” Thinking?
- Contradictions and god cannot logically co-exist.
- Naturalism and Logical Positivism?
- Anti-theism makes no logical sense?
- Psychological certainty and Epistemic certainty?
- Pragmatic Ethical/Axiology Driven Assumptions, Overcome the Weight of Solipsism Doubt
- Basics of my Methodological Rationalism Epistemology Approach
- Abhijit Naskar: Neuroscientist, Bestselling Author, Acclaimed Speaker on the Human Mind, and Peace Advocate
- Trying to Help Promote Knowledge: Philosophy and Science.
- Are aliens real? Think so than prove evidence, not a just conjecture hypothesis and inference speculations.
- Hammer of Truth: Yes, you too, have lots of beliefs…
- Challenging the Supremacy of Reason?
- Critical Thinking, What Does it Mean to Be Open to Learn?
- The Scientific Method and its Philosophy Axioms
- Flat Earth Mania: a debunked religious theory, given new life in the post-truth world
- When would skepticism NOT be reasonable?
- Atheistic Null Hypothesis: There is no God/Gods
- Scientific Values: fallibilism, realism, & rationalism
- Philosophical Skepticism, Solipsism and the Denial of Reality or Certainty
- Religious Faith as Evidence, is an Intellectual Reasoning Error
- Rationalist thinkers vs Skeptic thinkers
- Belief in god(s) May Involve Suppressing Analytical and Critical thinking
- Kurgans 6,000 years ago/dolmens 7,000 years ago: funeral, ritual, and other?
The Kurgan hypothesis (also known as the Kurgan theory or Kurgan model) or steppe theory is the most widely accepted proposal to identify the Proto-Indo-European homeland from which the Indo-European languages spread out throughout Europe and parts of Asia. It postulates that the people of a Kurgan culture in the Pontic steppe north of the Black Sea were the most likely speakers of the Proto-Indo-European language (PIE). The term is derived from the Russian kurgan, meaning tumulus or burial mound.
Researchers have identified a massive migration of Kurgan populations (Yamna culture) which went from the Russian steppes to the center of Europe some 4,500 years ago, favoring the expansion of Indo-European languages throughout the continent.
This was a time of astonishing creativity as city-states and empires emerged in a vast area stretching from the Mediterranean to the Indus Valley. The previous millennium had seen the emergence of advanced, urbanized civilizations, new bronze metallurgy extending the productivity of agricultural work, and highly developed ways of communication in the form of writing. In the 3rd millennium BC, the growth of these riches, both intellectually and physically, became a source of contention on a political stage, and rulers sought the accumulation of more wealth and more power. Along with this came the first appearances of mega-architecture, imperialism, organized absolutism and internal revolution. The civilizations of Sumer and Akkad in Mesopotamia became a collection of volatile city-states in which warfare was common. Uninterrupted conflicts drained all available resources, energies and populations. In this millennium, larger empires succeeded the last, and conquerors grew in stature until the great Sargon of Akkad pushed his empire to the whole of Mesopotamia and beyond. It would not be surpassed in size until Assyrian times 1,500 years later. In the Old Kingdom of Egypt, the Egyptian pyramids were constructed and would remain the tallest and largest human constructions for thousands of years. Also in Egypt, pharaohs began to posture themselves as living gods made of an essence different from that of other human beings. Even in Europe, which was still largely neolithic during the same period, the builders of megaliths were constructing giant monuments of their own. In the Near East and the Occident around 5,000 years ago and religion developed and advanced to roughly the ways we are somewhat familiar to a large amount, limits were being pushed by architects and rulers. Towards the close of the millennium, Egypt became the stage of the first popular revolution recorded in history. After lengthy wars, the Sumerians recognized the benefits of unification into a stable form of national government and became a relatively peaceful, well-organized, complex technocratic state called the 3rd dynasty of Ur. This dynasty was later to become involved with a wave of nomadic invaders known as the Amorites, who were to play a major role in the region during the following centuries. In the Near East and the Occident during the around 5,000 years ago and religion developed and advanced to roughly the ways we are somewhat familiar to a large amount, limits were being pushed by architects and rulers. Towards the close of the millennium, Egypt became the stage of the first popular revolution recorded in history. After lengthy wars, the Sumerians recognized the benefits of unification into a stable form of national government and became a relatively peaceful, well-organized, complex technocratic state called the 3rd dynasty of Ur. This dynasty was later to become involved with a wave of nomadic invaders known as the Amorites, who were to play a major role in the region during the following centuries. ref
Stars: Ancestors, Spirit Animals, and Deities (at least back to around 6,000 years ago)
- 5,750 years ago: The Proto-Semitic people emerged from a generally accepted urheimat in the Levant. The Proto-Semitic people would migrate throughout the Near East into Mesopotamia, Egypt, Ethiopia and the eastern shore of the Mediterranean.
- 5,700 years ago: Lothal: Indus Valley trade-port city in India.
- 5,650 years ago: Minoan culture appeared on Crete.
- 5,500 Years old birth of the State, the rise of Hierarchy, and the fall of Women’s status
- 5,300 years ago: The Indus Valley Civilization (IVC) was a Bronze Age civilization (3300–1300 BCE; mature period 2600–1900 BCE) in the northwestern region of the Indian subcontinent, noted for its cities built of brick, roadside drainage system and multi-storeyed houses, as well as for creating artifacts which could be linked to pre-vedic religions.
- 5,200 years ago: Helladic culture and Cycladic culture both emerge in Greece.
- 5,102 years ago: This was the beginning of Kaliyuga, a new age among the followers of Indian religions.
- 5,100 years ago: The initial form of Stonehenge was completed. The circular bank and ditch enclosure, about 110 metres (360 ft) across, may have been completed with a timber circle.
- 5,100 years ago: Newgrange, the 250,000 ton (226,796.2 tonne) passage tomb aligned to the winter solstice in Ireland, was built.
- 5,000 years ago: Unification of Upper and Lower Egypt.
- 5,000 years ago: First evidence of gold being used in the Middle East.
- 5,000 years ago: Vessels from Denmark
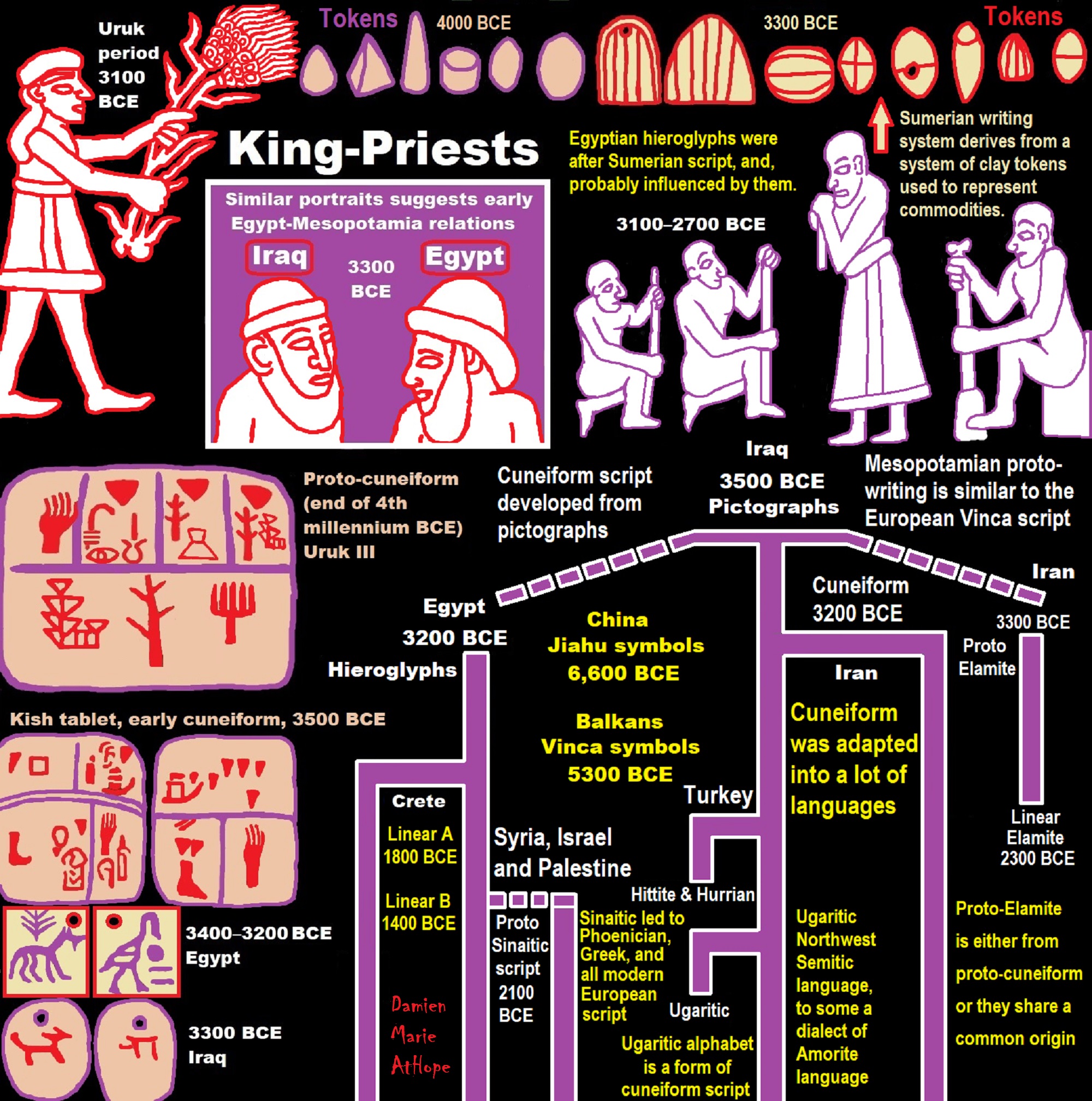
- 5,000 years ago: Sumerian Cuneiform emerged from the proto-literate Uruk period, allowing the codification of beliefs and creation of detailed historical religious records.
- 5,000 years ago: The second phase of Stonehenge was completed and appeared to function as the first enclosed cremation cemetery in the British Isles.
- 4,900 years ago: Beginning of the Early Dynastic Period I in Sumer.
- 4,900 years ago: Sumerianpictographs evolve into phonograms.
- 4,900 years ago: Mesopotamian wars of the Early Dynastic period.
- 4,900 years ago: Votive statues from the Square Temple of Eshnunna (modern Tell Ashmar, Iraq) were made.
- 4,900 years ago: Syria: Foundation of the city of Mari.
- 4,900 years ago: Semitic tribes occupy Assyria in northern part of the plain of Shinar and Akkad.
- 4,900 years ago: Phoenicians settle on Syrian coast, with centers at Tyre and Sidon.
- 4,900 years ago: Beginning of the period of the Sage Kings in China, also known as the Three Sovereigns and Five Emperors.
- 4,900 years ago: Ziggurats (multi-platform temples: 4,900 years old) to Pyramids (multi-platform tombs: 4,700 years old)
- 4,879 years ago: Rise of the Văn Lang Kingdom and the Hồng Bàng Dynasty in northern Viet Nam.
- 4,874 years ago: The 365-day calendar year was installed in ancient Egypt
- 4,852 years ago: The beginning of the period of the Three August Ones and Five Emperors in China.
- 4,832 years ago: Estimated germination of the Methuselah Tree, the oldest known living organism
- 4,807 years ago: Suggested date for an asteroid or comet impact occurring between Africa and Antarctica, around the time of a solar eclipse on May 10, based on an analysis of flood stories. Possibly causing the Burckle crater and Fenambosy Chevron.
- 4,800 years ago: Ur becomes one of the richest cities in Sumer
- 4,800 years ago: Harp Player, from Keros, Cyclades, was made. It is now at the Metropolitan Museum of Art, New York.
- 4,800 years ago: Iran: Creation of the Kingdom of Elam.
- 4,800 years ago: Seated Harp Player, from Keros, Cyclades, is made.
- 4,775 years ago: Second Dynasty wars in Ancient Egypt.
- 4,773 years ago: the 365-day calendar is introduced in Egypt.
- 4,750 years ago: End of the Early Dynastic I Period, and the beginning of the Early Dynastic II Period in Mesopotamia.
- 4,750 years ago: Estimated ending of the Cucuteni-Trypillian culture in the region of modern-day Romania, Moldova, and southwestern Ukraine
- 4,700 years ago: Germination of the Bristlecone pine tree “Methuselah“, one of the oldest known trees still living now.
- 4,700 years ago: Merit-Ptah is world’s first female physician mentioned by name.
- 4,700 years ago: Old Kingdom of Egypt begins. 3rd–6th Dynasties.
- 4,700 years ago: Mesoamericans begin to plant and domesticate maize.
- 4,697 years ago: The Yellow Emperor starts to reign in China.
- 4,685 years ago: Bull lyre from the tomb of Queen Puabi, Ur (modern Muqaiyir, Iraq) was made.
- 4,640 years ago: The cultivation and weaving of silk starts to be a closely guarded secret in China.
- 4,630 years ago: Imhotep, Vizier of Egypt, constructs the Pyramid of Djoser The Djoser pyramid is a step pyramid (or proto-pyramid) is considered to be the earliest large-scale cut stone construction and was thought to function in both life and the afterlife, which was sealed with a 3.5 ton block after the burial. The symbolism of the step pyramid form, which did not survive the 3rd Dynasty, is unknown, but it has been suggested that it may be a monumental symbol of the crown, especially the royal mortuary cult, since seven small step pyramids (not tombs) were built in the provinces.
- 4,627 years ago: Construction of the Caral metropolis in Peru
- 4,600 years ago: Mature Harappan phase of the Indus Valley Civilisation begins. The cities of Harappa and Mohenjo-daro become large metropolises and the civilization expands to over 2,500 cities and settlements across the whole of Pakistan, much of northern India, and parts of Afghanistan and Iran, covering a region of around one million square miles, which was larger than the land area of its contemporaries Egypt and Mesopotamia combined, and also had superior urban planning and sewage systems. The civilization began using the mature Indus script for its writing system.
- 4,600 years ago: End of the Early Dynastic II Period and the beginning of the Early Dynastic IIIa Period in Mesopotamia.
- 4,600 years ago: Founding of the Chalcolithic Iberian civilizations of Los Millares and Zambujal.
- 4,600 years ago: the Indus Valley Civilisation rises to become a powerful civilization.
- 4,600 years ago: Pre-Palace Period, phase I, in Crete
- 4,600 years ago: Wild horses still provide hunting feasts in Denmark. (Clutton-Brock)
- 4,600 years ago: Large water tank, possibly a public or ritual bathing area, Mohenjo-daro, Indus Valley Civilisation, is made.
- 4,600 years ago: Butmir culture existed in Butmir, near Ilidža, Bosnia and Herzegovina, dating from the Neolithic. It is characterized by its unique pottery, and is one of the best researched European cultures from 2600-2400 BC.
- 4,600 years ago: Unified Indus Valley Civilisation.
- 4,550 years ago: Estimated date of completion of the Great Pyramid of Giza.
- 4,550 years ago: Mesannepada is king of Ur (followed by his son, A-annepadda) who founds the First Dynasty of Ur and overthrows the last king of Uruk, as well as Mesilim of Kish.
- 4,550 years ago:: Great Lyre with bull’s head, from the tomb of King Meskalamdug, Ur (modern Muqaiyir, Iraq) is made.
- 4,500 years ago: Excavation and development of the Hypogeum of Ħal-Saflieni at Paola, Malta, a subterranean temple complex subsequently used as a necropolis.
- 4,500 years ago: The legendary line of Three Sovereigns and Five Emperors of China is founded by the Yellow Emperor.
- 4,500 years ago: the construction of the stone circle at Stonehenge begins and continues for the next five hundred years.
- 4,500 years ago: Rice was first introduced to Malaysia
- 4,500 years ago: Scribal schools flourish throughout Sumer.
- 4,500 years ago: Assyria is established.
- 4,500 years ago: Cylinder seal from Sumer and its impression are made. It is now in the Metropolitan Museum of Art, New York.
- 4,500 years ago: Excavation and development of the Hypogeum of Ħal-Saflieni at Paola, Malta, a subterranean temple complex subsequently used as a necropolis.
- 4,500 years ago: Valley Temple of Khafra, Giza, is built.
- 4,500 years ago: Khafra from Giza Valley, Temple of Khafra is made. Fourth Dynasty of Egypt. Discovered by Auguste Mariette. It is now kept in Egyptian Museum, Cairo.
- 4,500 years ago: Mohenjo-daro is about 7 square miles (18 km2) in size and has a population of c. 20,000 to 50,000.
- 4, 500 years ago: Incised panel “Frying pan”, from Syros, Cyclades is made.
- 4,500 years ago: Two figures of women, from the Cyclades, are made.
- 4,494 years ago: End of Fourth Dynasty, start of Fifth Dynasty in Egypt. Construction of the Pyramids begins.
- 4,494 years ago: “Sculptors at work”, relief from Saqqara, Fifth Dynasty. It is now at Egyptian Museum, Cairo, Egypt.
- 4,494 years ago: The Seated Scribe, a sculpture found at Saqqara, Fifth Dynasty of Egypt is made.
- 4,494 years ago: The first of the oldest surviving religious texts, the Pyramid Texts, was composed in Ancient Egypt.
- 4,492 years ago: Traditional date for the legendary foundation of Armenia by Hayk.
- 4,492 years ago: The Armenian patriarch Hayk defeats the Babylonian king Bel (legendary account) and Hayk founds Armenia.
- 4,474 years ago: Golden age of Ur in Mesopotamia.
- 4,450 years ago: End of the Early Dynastic IIIa Period and beginning of the Early Dynastic IIIb Period in Sumer.
- 4,450 years ago: Kish is lost to Hamazi tribesmen of the Kurdistan mountains; Elam under the Awan dynasty occupies parts of Sumer.
- 4,419 years ago: Neferefre is pharaoh
- 4,410 years ago: By this time, kings in Sumer have ceased to be automatically high priests of the city deity. Infiltration and conquest of Mesopotamia by ancient Semitic-speaking peoplesbegins.
- 4,400 years ago: Construction of Stonehenge
- 4,400 years ago: Megalithic culture begins to spread through Europe and the western Mediterranean.
- 4,400 years ago: Earliest signs of Corded Ware culture from the Caucasus.
- 4,400 years ago: Southeastern Spain is settled from the Mediterranean, by people using Prehistoric Egyptian-style pottery.
- 4,400 years ago: Amorites and Canaanites occupy Syria and Lebanon.
- 4,334 years ago: Sargon of Akkad conquers Mesopotamia, establishing the Akkadian Empire.
- 4,334 years ago: City of Lothal founded under the Indus Valley Civilisation.
- 4,333 years ago: According to the Korean creation story, Dangun Wanggeom established the first Korean Empire, Gojoseon
- 4,300 years ago: C-Group pastoralists arrive in Nubia.
- 4,300 years ago: Megalithic, Corded Ware culture and the Beaker flourish in Europe.
- 4,300 years ago: Sumerian poetry, lamenting the death of Tammuz, the shepherd god.
- 4,300 years ago: Sumerian cuneiform writing reduces pictographs still in use to about 550 BC.
- 4,300 years ago: Major religious festival in Sumeria celebrates the victory of god of spring over goddess of chaos.
- 4,300 years ago: Earliest Trojan culture.
- 4,300 years ago: Beginning of the Pengtoushan culture in China.
- 4,300 years ago: Indus Valley Civilization (Harappan) flourishing in modern day eastern Pakistan – western India.
- 4,300 years ago: Metals start to be used in Northern Europe.
- 4,300 years ago: Unetice culture emerges in the modern day Czech Republic.
- 4,300 years ago: Disk of Enheduanna, from Ur, (modern Muqaiyir, Iraq) is made.
- 4,300 years ago: “Head of a man from Nineveh” (modern Kuyunjik, Iraq) is made.
- 4,285 years ago: Enheduanna, high priestess of the moon god Nanna in Ur, was born.
- 4,254 years ago: Stela of Naram-Sin, probably from Sippar, discovered in Susa (modern Shush, Iran), is made.
- 4,250 years ago: Earliest evidence of maize cultivation in Central America.
- 4,240 years ago: Akkad, capital of the Akkadian Empire, becomes the largest city in the world, surpassing Memphis, capital of Egypt.
- 4,220 years ago: Scord of Brouster farmstead established in Shetland, Scotland
- 4.2 kiloyear event– a severe aridification event that probably lasted the entire 22nd century BC and caused the collapse of several Old World civilizations.
- 4,217 years ago: Nomadic invasions of Akkad.
- 4,200 years ago: The Minoan Civilization developed in Crete. Citizens worshipped a variety of goddesses.
- 4,150 years ago: The earliest surviving versions of the Sumerian Epic of Gilgamesh—originally titled He who Saw the Deep (Sha naqba īmuru) or Surpassing All Other Kings (Shūtur eli sharrī)—were written.
- 4,104 years ago: Approximate date of the Biblical flood according to the Hebrew Calendar.
- 4,070 years ago: Xia Dynasty, first Chinese dynasty and government system established.
- 4,000 years ago: Kultepe? An archaeological site with a 4,000 years old women’s rights document.
- 3,700 years ago: The oldest of the Hindu Vedas (scriptures), the Rig Veda was composed.
- 3,600 years ago: The ancient development of Stonehenge came to an end.
- 3,500 years ago: The Vedic Age began in India after the collapse of the Indus Valley Civilisation.
- 3,450 years ago: This is the traditionally accepted period in which, according to legend, the Israelite lawgiver Moses gave the Ten Commandments.
- 3,351 years ago: The reign of Akhenaten, sometimes credited with starting the earliest known recorded monotheistic religion, in Ancient Egypt
- 3,300 years ago: The “standard” Akkadian version of the Epic of Gilgamesh was edited by Sin-liqe-unninni.
- 3,250 years ago: The Upanishads (Vedic texts) were composed, containing the earliest emergence of some of the central religious concepts of Hinduism, Buddhism and Jainism. ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref
Understanding Religion Evolution:
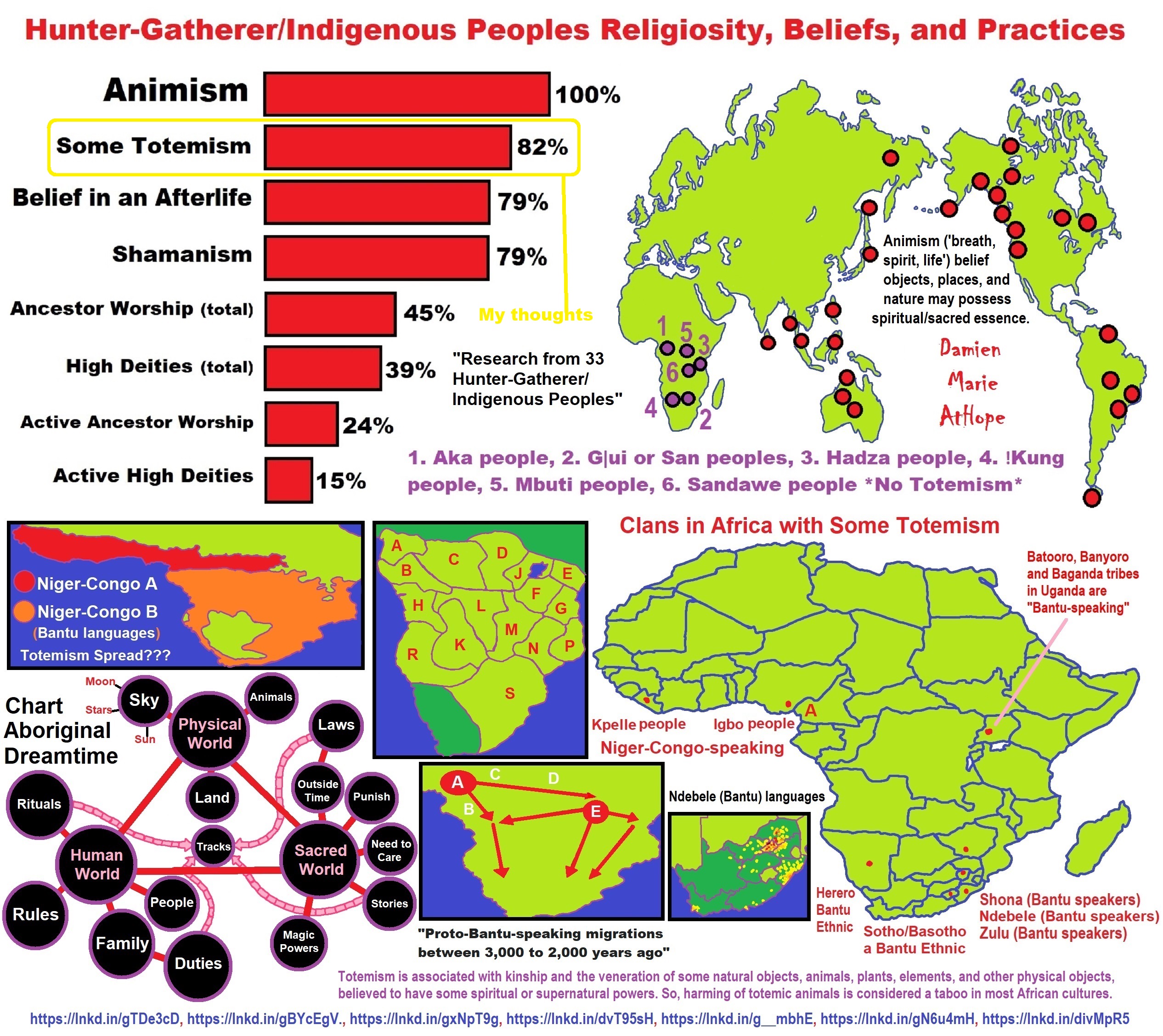
- Animism (Africa: 100,000 years ago), (Animism | Britannica.com)
- Totemism (Europe: 50,000 years ago), (Totemism – Anthropology)
- Shamanism (Siberia: 30,000 years ago), (Shamanism | Britannica.com)
- Paganism (Turkey: 12,000 years ago), (BBC – Religion: Paganism)
- Progressed organized religion (Egypt: 5,000 years ago), (Prehistoric Egypt 40,000 years ago to The First Dynasty 5,150 years ago)
“Religion is an Evolved Product”
Religions continuing in our modern world, full of science and facts, should be seen as little more than a set of irrational conspiracy theories of reality. Nothing more than a confused reality made up of unscientific echoes from man’s ancient past. Rational thinkers must ask themselves, why continue to believe in religions’ stories? Religion myths which are nothing more than childlike stories and obsolete tales once used to explain how the world works, acting like magic was needed when it was always only nature. These childlike religious stories should not even be taken seriously, but sadly too often they are. Often without realizing it, we accumulate beliefs that we allow to negatively influence our lives. In order to bring about awareness, we need to be willing to alter skewed beliefs. Rational thinkers must examine the facts instead of blindly following beliefs or faith.
Below is a collection of researched information such as archaeology, history, linguistics, genetics, art, science, sociology, geography, psychology, philosophy, theology, biology, and zoology. It will make you question your beliefs with information, inquiries, and ideas to ponder and expand on. The two main goals are to expose the evolution of religion starting 100,000 years ago and to offer challenges to remove the rationale of faith. It is like an intervention for belief in myths that have plagued humankind for way too long. We often think we know what truth is nevertheless this can be but a vantage point away from losing credibility if we are not willing to follow valid and reliable reason and evidence. The door of reason opens not once but many times. Come on a journey to free thought where the war is against ignorance and the victor is a rational mind.
If you are a religious believer, may I remind you that faith in the acquisition of knowledge is not a valid method worth believing in. Because, what proof is “faith”, of anything religion claims by faith, as many people have different faith even in the same religion?


Animism: Respecting the Living World by Graham Harvey
“How have human cultures engaged with and thought about animals, plants, rocks, clouds, and other elements in their natural surroundings? Do animals and other natural objects have a spirit or soul? What is their relationship to humans? In this new study, Graham Harvey explores current and past animistic beliefs and practices of Native Americans, Maori, Aboriginal Australians, and eco-pagans. He considers the varieties of animism found in these cultures as well as their shared desire to live respectfully within larger natural communities. Drawing on his extensive casework, Harvey also considers the linguistic, performative, ecological, and activist implications of these different animisms.” ref


My thoughts on Religion Evolution with external links for more info:
- (Pre-Animism Africa mainly, but also Europe, and Asia at least 300,000 years ago), (Pre-Animism – Oxford Dictionaries)
- (Animism Africa around 100,000 years ago), (Animism – Britannica.com)
- (Totemism Europe around 50,000 years ago), (Totemism – Anthropology)
- (Shamanism Siberia around 30,000 years ago), (Shamanism – Britannica.com)
- (Paganism Turkey around 12,000 years ago), (Paganism – BBC Religion)
- (Progressed Organized Religion “Institutional Religion” Egypt around 5,000 years ago), (Ancient Egyptian Religion – Britannica.com)
- (CURRENT “World” RELIGIONS after 4,000 years ago) (Origin of Major Religions – Sacred Texts)
- (Early Atheistic Doubting at least by 2,600 years ago) (History of Atheism – Wikipedia)
“Religion is an Evolved Product” and Yes, Religion is Like Fear Given Wings…
Atheists talk about gods and religions for the same reason doctors talk about cancer, they are looking for a cure, or a firefighter talks about fires because they burn people and they care to stop them. We atheists too often feel a need to help the victims of mental slavery, held in the bondage that is the false beliefs of gods and the conspiracy theories of reality found in religions.
Understanding Religion Evolution:
- Pre-Animism (at least 300,000 years ago)
- Animism (Africa: 100,000 years ago)
- Totemism (Europe: 50,000 years ago)
- Shamanism (Siberia: 30,000 years ago)
- Paganism (Turkey: 12,000 years ago)
- Progressed organized religion (Egypt: 5,000 years ago), (Egypt, the First Dynasty 5,150 years ago)
- CURRENT “World” RELIGIONS (after 4,000 years ago)
- Early Atheistic Doubting (at least by 2,600 years ago)
“An Archaeological/Anthropological Understanding of Religion Evolution”
It seems ancient peoples had to survived amazing threats in a “dangerous universe (by superstition perceived as good and evil),” and human “immorality or imperfection of the soul” which was thought to affect the still living, leading to ancestor worship. This ancestor worship presumably led to the belief in supernatural beings, and then some of these were turned into the belief in gods. This feeble myth called gods were just a human conceived “made from nothing into something over and over, changing, again and again, taking on more as they evolve, all the while they are thought to be special,” but it is just supernatural animistic spirit-belief perceived as sacred.
Quick Evolution of Religion?
Pre-Animism (at least 300,000 years ago) pre-religion is a beginning that evolves into later Animism. So, Religion as we think of it, to me, all starts in a general way with Animism (Africa: 100,000 years ago) (theoretical belief in supernatural powers/spirits), then this is physically expressed in or with Totemism (Europe: 50,000 years ago) (theoretical belief in mythical relationship with powers/spirits through a totem item), which then enlists a full-time specific person to do this worship and believed interacting Shamanism (Siberia/Russia: 30,000 years ago) (theoretical belief in access and influence with spirits through ritual), and then there is the further employment of myths and gods added to all the above giving you Paganism (Turkey: 12,000 years ago) (often a lot more nature-based than most current top world religions, thus hinting to their close link to more ancient religious thinking it stems from). My hypothesis is expressed with an explanation of the building of a theatrical house (modern religions development). Progressed organized religion (Egypt: 5,000 years ago) with CURRENT “World” RELIGIONS (after 4,000 years ago).
Historically, in large city-state societies (such as Egypt or Iraq) starting around 5,000 years ago culminated to make religion something kind of new, a sociocultural-governmental-religious monarchy, where all or at least many of the people of such large city-state societies seem familiar with and committed to the existence of “religion” as the integrated life identity package of control dynamics with a fixed closed magical doctrine, but this juggernaut integrated religion identity package of Dogmatic-Propaganda certainly did not exist or if developed to an extent it was highly limited in most smaller prehistoric societies as they seem to lack most of the strong control dynamics with a fixed closed magical doctrine (magical beliefs could be at times be added or removed). Many people just want to see developed religious dynamics everywhere even if it is not. Instead, all that is found is largely fragments until the domestication of religion.
Religions, as we think of them today, are a new fad, even if they go back to around 6,000 years in the timeline of human existence, this amounts to almost nothing when seen in the long slow evolution of religion at least around 70,000 years ago with one of the oldest ritual worship. Stone Snake of South Africa: “first human worship” 70,000 years ago. This message of how religion and gods among them are clearly a man-made thing that was developed slowly as it was invented and then implemented peace by peace discrediting them all. Which seems to be a simple point some are just not grasping how devastating to any claims of truth when we can see the lie clearly in the archeological sites.
I wish people fought as hard for the actual values as they fight for the group/clan names political or otherwise they think support values. Every amount spent on war is theft to children in need of food or the homeless kept from shelter.
Here are several of my blog posts on history:
- To Find Truth You Must First Look
- (Magdalenian/Iberomaurusian) Connections to the First Paganists of the early Neolithic Near East Dating from around 17,000 to 12,000 Years Ago
- Natufians: an Ancient People at the Origins of Agriculture and Sedentary Life
- Possible Clan Leader/Special “MALE” Ancestor Totem Poles At Least 13,500 years ago?
- Jewish People with DNA at least 13,200 years old, Judaism, and the Origins of Some of its Ideas
- Baltic Reindeer Hunters: Swiderian, Lyngby, Ahrensburgian, and Krasnosillya cultures 12,020 to 11,020 years ago are evidence of powerful migratory waves during the last 13,000 years and a genetic link to Saami and the Finno-Ugric peoples.
- The Rise of Inequality: patriarchy and state hierarchy inequality
- Fertile Crescent 12,500 – 9,500 Years Ago: fertility and death cult belief system?
- 12,400 – 11,700 Years Ago – Kortik Tepe (Turkey) Pre/early-Agriculture Cultic Ritualism
- Ritualistic Bird Symbolism at Gobekli Tepe and its “Ancestor Cult”
- Male-Homosexual (female-like) / Trans-woman (female) Seated Figurine from Gobekli Tepe
- Could a 12,000-year-old Bull Geoglyph at Göbekli Tepe relate to older Bull and Female Art 25,000 years ago and Later Goddess and the Bull cults like Catal Huyuk?
- Sedentism and the Creation of goddesses around 12,000 years ago as well as male gods after 7,000 years ago.
- Alcohol, where Agriculture and Religion Become one? Such as Gobekli Tepe’s Ritualistic use of Grain as Food and Ritual Drink
- Neolithic Ritual Sites with T-Pillars and other Cultic Pillars
- Paganism: Goddesses around 12,000 years ago then Male Gods after 7,000 years ago
- First Patriarchy: Split of Women’s Status around 12,000 years ago & First Hierarchy: fall of Women’s Status around 5,000 years ago.
- Natufians: an Ancient People at the Origins of Agriculture and Sedentary Life
- J DNA and the Spread of Agricultural Religion (paganism)
- Paganism: an approximately 12,000-year-old belief system
- Paganism 12,000 years old: related to “Anarchism and Socialism” (Pre-Capitalism)
- Shaman burial in Israel 12,000 years ago and the Shamanism Phenomena
- Need to Mythicized: gods and goddesses
- 12,000 – 7,000 Years Ago – Paleo-Indian Culture (The Americas)
- 12,000 – 2,000 Years Ago – Indigenous-Scandinavians (Nordic)
- Norse did not wear helmets with horns?
- Pre-Pottery Neolithic Skull Cult around 11,500 to 8,400 Years Ago?
- 10,400 – 10,100 Years Ago, in Turkey the Nevail Cori Religious Settlement
- 9,000-6,500 Years Old Submerged Pre-Pottery/Pottery Neolithic Ritual Settlements off Israel’s Coast
- Catal Huyuk “first religious designed city” around 9,500 to 7,700 years ago (Turkey)
- Cultic Hunting at Catal Huyuk “first religious designed city”
- Special Items and Art as well as Special Elite Burials at Catal Huyuk
- New Rituals and Violence with the appearance of Pottery and People?
- Haplogroup N and its related Uralic Languages and Cultures
- Ainu people, Sámi people, Native Americans, the Ancient North Eurasians, and Paganistic-Shamanism with Totemism
- Ideas, Technology and People from Turkey, Europe, to China and Back again 9,000 to 5,000 years ago?
- First Pottery of Europe and the Related Cultures
- 9,000 years old Neolithic Artifacts Judean Desert and Hills Israel
- 9,000-7,000 years-old Sex and Death Rituals: Cult Sites in Israel, Jordan, and the Sinai
- 9,000-8500 year old Horned Female shaman Bad Dürrenberg Germany
- Neolithic Jewelry and the Spread of Farming in Europe Emerging out of West Turkey
- 8,600-year-old Tortoise Shells in Neolithic graves in central China have Early Writing and Shamanism
- Swing of the Mace: the rise of Elite, Forced Authority, and Inequality begin to Emerge 8,500 years ago?
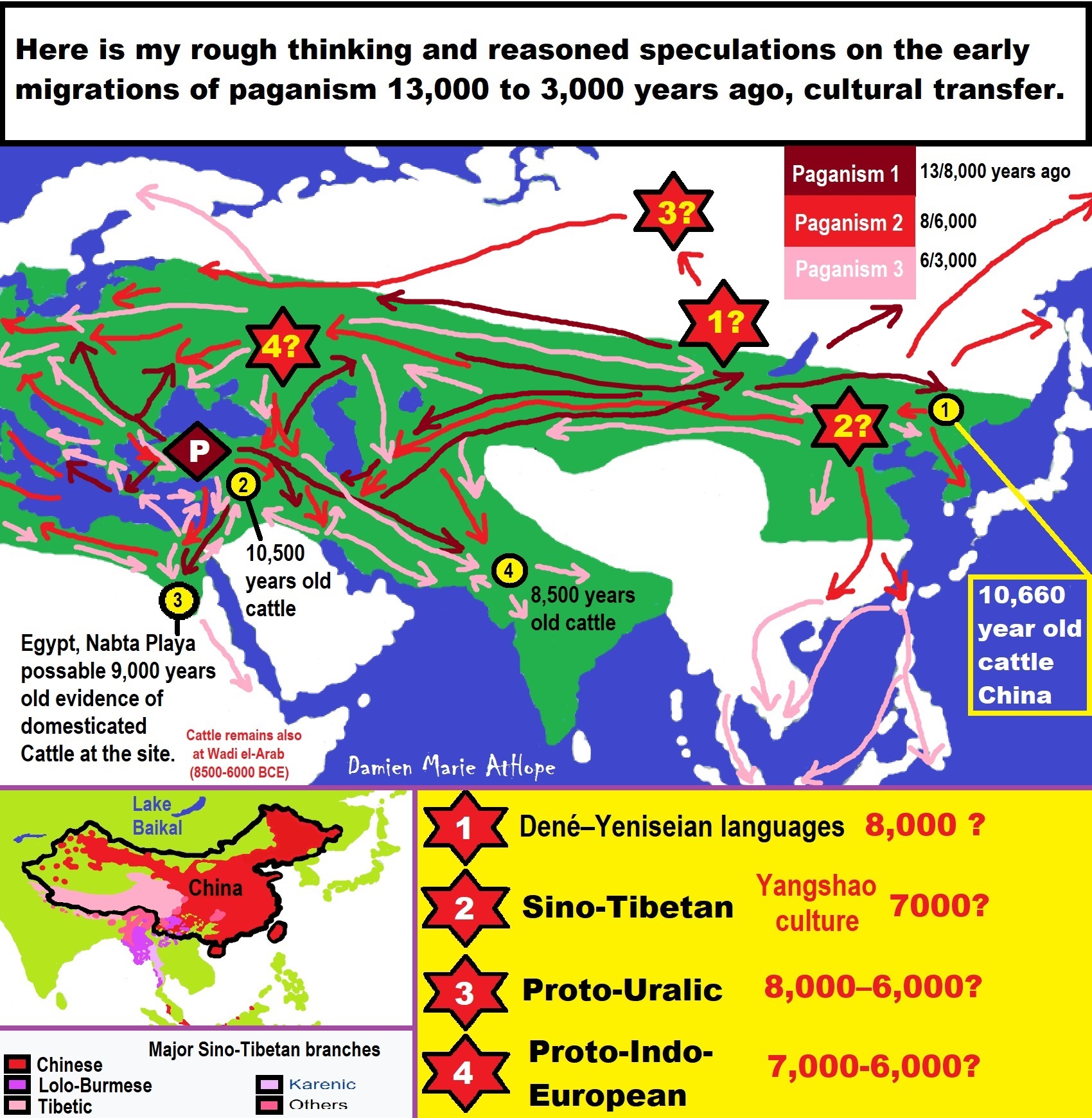
- Migrations and Changing Europeans Beginning around 8,000 Years Ago
- My “Steppe-Anatolian-Kurgan hypothesis” 8,000/7,000 years ago
- Around 8,000-year-old Shared Idea of the Mistress of Animals, “Ritual” Motif
- Pre-Columbian Red-Paint (red ochre) Maritime Archaic Culture 8,000-3,000 years ago
- 7,522-6,522 years ago Linear Pottery culture which I think relates to Arcane Capitalism’s origins
- Arcane Capitalism: Primitive socialism, Primitive capital, Private ownership, Means of production, Market capitalism, Class discrimination, and Petite bourgeoisie (smaller capitalists)
- 7,500-4,750 years old Ritualistic Cucuteni-Trypillian culture of Moldova, Romania, and Ukraine
- Roots of a changing early society 7,200-6,700 years ago Jordan and Israel
- Agriculture religion (Paganism) with farming reached Britain between about 7,000 to 6,500 or so years ago and seemingly expressed in things like Western Europe’s Long Barrows
- My Thoughts on Possible Migrations of “R” DNA and Proto-Indo-European?
- “Millet” Spreading from China 7,022 years ago to Europe and related Language may have Spread with it leading to Proto-Indo-European
- Proto-Indo-European (PIE), ancestor of Indo-European languages: DNA, Society, Language, and Mythology
- The Dnieper–Donets culture and Asian varieties of Millet from China to the Black Sea region of Europe by 7,022 years ago
- Kurgan 6,000 years ago/dolmens 7,000 years ago: funeral, ritual, and other?
- 7,020 to 6,020-year-old Proto-Indo-European Homeland of Urheimat or proposed home of their Language and Religion
- Ancient Megaliths: Kurgan, Ziggurat, Pyramid, Menhir, Trilithon, Dolman, Kromlech, and Kromlech of Trilithons
- The Mytheme of Ancient North Eurasian Sacred-Dog belief and similar motifs are found in Indo-European, Native American, and Siberian comparative mythology
- Elite Power Accumulation: Ancient Trade, Tokens, Writing, Wealth, Merchants, and Priest-Kings
- Sacred Mounds, Mountains, Kurgans, and Pyramids may hold deep connections?
- Between 7,000-5,000 Years ago, rise of unequal hierarchy elite, leading to a “birth of the State” or worship of power, strong new sexism, oppression of non-elites, and the fall of Women’s equal status
- Paganism 7,000-5,000 years old: related to “Anarchism and Socialism” (Capitalism) (World War 0) Elite & their slaves
- Hell and Underworld mythologies starting maybe as far back as 7,000 to 5,000 years ago with the Proto-Indo-Europeans?
- The First Expression of the Male God around 7,000 years ago?
- White (light complexion skin) Bigotry and Sexism started 7,000 years ago?
- Around 7,000-year-old Shared Idea of the Divine Bird (Tutelary and/or Trickster spirit/deity), “Ritual” Motif
- Nekhbet an Ancient Egyptian Vulture Goddess and Tutelary Deity
- 6,720 to 4,920 years old Ritualistic Hongshan Culture of Inner Mongolia with 5,000-year-old Pyramid Mounds and Temples
- First proto-king in the Balkans, Varna culture around 6,500 years ago?
- 6,500–5,800 years ago in Israel Late Chalcolithic (Copper Age) Period in the Southern Levant Seems to Express Northern Levant Migrations, Cultural and Religious Transfer
- KING OF BEASTS: Master of Animals “Ritual” Motif, around 6,000 years old or older…
- Around 6000-year-old Shared Idea of the Solid Wheel & the Spoked Wheel-Shaped Ritual Motif
- “The Ghassulian Star,” a mysterious 6,000-year-old mural from Jordan; a Proto-Star of Ishtar, Star of Inanna or Star of Venus?
- Religious/Ritual Ideas, including goddesses and gods as well as ritual mounds or pyramids from Northeastern Asia at least 6,000 years old, seemingly filtering to Iran, Iraq, the Mediterranean, Europe, Egypt, and the Americas?
- Maykop (5,720–5,020 years ago) Caucasus region Bronze Age culture-related to Copper Age farmers from the south, influenced by the Ubaid period and Leyla-Tepe culture, as well as influencing the Kura-Araxes culture
- 5-600-year-old Tomb, Mummy, and First Bearded Male Figurine in a Grave
- Kura-Araxes Cultural 5,520 to 4,470 years old DNA traces to the Canaanites, Arabs, and Jews
- Minoan/Cretan (Keftiu) Civilization and Religion around 5,520 to 3,120 years ago
- Evolution Of Science at least by 5,500 years ago
- 5,500 Years old birth of the State, the rise of Hierarchy, and the fall of Women’s status
- “Jiroft culture” 5,100 – 4,200 years ago and the History of Iran
- Stonehenge: Paganistic Burial and Astrological Ritual Complex, England (5,100-3,600 years ago)
- Around 5,000-year-old Shared Idea of the “Tree of Life” Ritual Motif
- Complex rituals for elite, seen from China to Egypt, at least by 5,000 years ago
- Around 5,000 years ago: “Birth of the State” where Religion gets Military Power and Influence
- The Center of the World “Axis Mundi” and/or “Sacred Mountains” Mythology Could Relate to the Altai Mountains, Heart of the Steppe
- Progressed organized religion starts, an approximately 5,000-year-old belief system
- China’s Civilization between 5,000-3,000 years ago, was a time of war and class struggle, violent transition from free clans to a Slave or Elite society
- Origin of Logics is Naturalistic Observation at least by around 5,000 years ago.
- Paganism 5,000 years old: progressed organized religion and the state: related to “Anarchism and Socialism” (Kings and the Rise of the State)
- Ziggurats (multi-platform temples: 4,900 years old) to Pyramids (multi-platform tombs: 4,700 years old)
- Did a 4,520–4,420-year-old Volcano In Turkey Inspire the Bible God?
- Finland’s Horned Shaman and Pre-Horned-God at least 4,500 years ago?
- 4,000-year-Old Dolmens in Israel: A Connected Dolmen Religious Phenomenon?
- Creation myths: From chaos, Ex nihilo, Earth-diver, Emergence, World egg, and World parent
- Bronze Age “Ritual” connections of the Bell Beaker culture with the Corded Ware/Single Grave culture, which were related to the Yamnaya culture and Proto-Indo-European Languages/Religions
- Low Gods (Earth/ Tutelary deity), High Gods (Sky/Supreme deity), and Moralistic Gods (Deity enforcement/divine order)
- The exchange of people, ideas, and material-culture including, to me, the new god (Sky Father) and goddess (Earth Mother) religion between the Cucuteni-Trypillians and others which is then spread far and wide
- Koryaks: Indigenous People of the Russian Far East and Big Raven myths also found in Tlingit, Haida, Tsimshian, and other Indigenous People of North America
- 42 Principles Of Maat (Egyptian Goddess of the justice) around 4,400 years ago, 2000 Years Before Ten Commandments
- “Happy Easter” Well Happy Eostre/Ishter
- 4,320-3,820 years old “Shimao” (North China) site with Totemistic-Shamanistic Paganism and a Stepped Pyramid
- 4,250 to 3,400 Year old Stonehenge from Russia: Arkaim?
- 4,100-year-old beaker with medicinal & flowering plants in a grave of a woman in Scotland
- Early European Farmer ancestry, Kelif el Boroud people with the Cardial Ware culture, and the Bell Beaker culture Paganists too, spread into North Africa, then to the Canary Islands off West Africa
- Flood Accounts: Gilgamesh epic (4,100 years ago) Noah in Genesis (2,600 years ago)
- Paganism 4,000 years old: related to “Anarchism and Socialism” (First Moralistic gods, then the Origin time of Monotheism)
- When was the beginning: TIMELINE OF CURRENT RELIGIONS, which start around 4,000 years ago.
- Early Religions Thought to Express Proto-Monotheistic Systems around 4,000 years ago
- Kultepe? An archaeological site with a 4,000 years old women’s rights document.
- Single God Religions (Monotheism) = “Man-o-theism” started around 4,000 years ago with the Great Sky Spirit/God Tiān (天)?
- Confucianism’s Tiān (Shangdi god 4,000 years old): Supernaturalism, Pantheism or Theism?
- Yes, Your Male God is Ridiculous
- Mythology, a Lunar Deity is a Goddess or God of the Moon
- Sacred Land, Hills, and Mountains: Sami Mythology (Paganistic Shamanism)
- Horse Worship/Sacrifice: mythical union of Ruling Elite/Kingship and the Horse
- The Amorite/Amurru people’s God Amurru “Lord of the Steppe”, relates to the Origins of the Bible God?
- Bronze Age Exotic Trade Routes Spread Quite Far as well as Spread Religious Ideas with Them
- Sami and the Northern Indigenous Peoples Landscape, Language, and its Connection to Religion
- Prototype of Ancient Analemmatic Sundials around 3,900-3,150 years ago and a Possible Solar Connection to gods?
- Judaism is around 3,450 or 3,250 years old. (“Paleo-Hebrew” 3,000 years ago and Torah 2,500 years ago)
- The Weakening of Ancient Trade and the Strengthening of Religions around 3000 years ago?
- Are you aware that there are religions that worship women gods, explain now religion tears women down?
- Animistic, Totemistic, and Paganistic Superstition Origins of bible god and the bible’s Religion.
- Myths and Folklore: “Trickster gods and goddesses”
- Jews, Judaism, and the Origins of Some of its Ideas
- An Old Branch of Religion Still Giving Fruit: Sacred Trees
- Dating the BIBLE: naming names and telling times (written less than 3,000 years ago, provable to 2,200 years ago)
- Did a Volcano Inspire the bible god?
- The Amorite/Amurru people’s God Amurru “Lord of the Steppe”, relates to the Origins of the Bible God?
- Dené–Yeniseian language, Old Copper Complex, and Pre-Columbian Mound Builders?
- No “dinosaurs and humans didn’t exist together just because some think they are in the bible itself”
- Sacred Shit and Sacred Animals?
- Everyone Killed in the Bible Flood? “Nephilim” (giants)?
- Hey, Damien dude, I have a question for you regarding “the bible” Exodus.
- Archaeology Disproves the Bible
- Bible Battle, Just More, Bible Babble
- The Jericho Conquest lie?
- Canaanites and Israelites?
- Accurate Account on how did Christianity Began?
- Let’s talk about Christianity.
- So the 10 commandments isn’t anything to go by either right?
- Misinformed christian
- Debunking Jesus?
- Paulism vs Jesus
- Ok, you seem confused so let’s talk about Buddhism.
- Unacknowledged Buddhism: Gods, Savior, Demons, Rebirth, Heavens, Hells, and Terrorism
- His Foolishness The Dalai Lama
- Yin and Yang is sexist with an ORIGIN around 2,300 years ago?
- I Believe Archaeology, not Myths & Why Not, as the Religious Myths Already Violate Reason!
- Archaeological, Scientific, & Philosophic evidence shows the god myth is man-made nonsense.
- Aquatic Ape Theory/Hypothesis? As Always, Just Pseudoscience.
- Ancient Aliens Conspiracy Theorists are Pseudohistorians
- The Pseudohistoric and Pseudoscientific claims about “Bakoni Ruins” of South Africa
- Why do people think Religion is much more than supernaturalism and superstitionism?
- Religion is an Evolved Product
- Was the Value of Ancient Women Different?
- 1000 to 1100 CE, human sacrifice Cahokia Mounds a pre-Columbian Native American site
- Feminist atheists as far back as the 1800s?
- Promoting Religion as Real is Mentally Harmful to a Flourishing Humanity
- Screw All Religions and Their Toxic lies, they are all fraud
- Forget Religions’ Unfounded Myths, I Have Substantiated “Archaeology Facts.”
- Religion Dispersal throughout the World
- I Hate Religion Just as I Hate all Pseudoscience
- Exposing Scientology, Eckankar, Wicca and Other Nonsense?
- Main deity or religious belief systems
- Quit Trying to Invent Your God From the Scraps of Science.
- Archaeological, Scientific, & Philosophic evidence shows the god myth is man-made nonsense.
- Ancient Alien Conspiracy Theorists: Misunderstanding, Rhetoric, Misinformation, Fabrications, and Lies
- Misinformation, Distortion, and Pseudoscience in Talking with a Christian Creationist
- Judging the Lack of Goodness in Gods, Even the Norse God Odin
- Challenging the Belief in God-like Aliens and Gods in General
- A Challenge to Christian use of Torture Devices?
- Yes, Hinduism is a Religion
- Trump is One of the Most Reactionary Forces of Far-right Christian Extremism
- Was the Bull Head a Symbol of God? Yes!
- Primate Death Rituals
- Christian – “God and Christianity are objectively true”
- Australopithecus afarensis Death Ritual?
- You Claim Global Warming is a Hoax?
- Doubter of Science and Defamer of Atheists?
- I think that sounds like the Bible?
- History of the Antifa (“anti-fascist”) Movements
- Indianapolis Anti-Blasphemy Laws #Free Soheil Rally
- Damien, you repeat the golden rule in so many forms then you say religion is dogmatic?
- Science is a Trustable Methodology whereas Faith is not Trustable at all!
- Was I ever a believer, before I was an atheist?
- Atheists rise in reason
- Mistrust of science?
- Open to Talking About the Definition of ‘God’? But first, we address Faith.
- ‘United Monarchy’ full of splendor and power – Saul, David, and Solomon? Most likely not.
- Is there EXODUS ARCHAEOLOGY? The short answer is “no.”
- Lacking Proof of Bigfoots, Unicorns, and Gods is Just a Lack of Research?
- Religion and Politics: Faith Beliefs vs. Rational Thinking
- Hammer of Truth that lying pig RELIGION: challenged by an archaeologist
- “The Hammer of Truth” -ontology question- What do You Mean by That?
- Navigation of a bad argument: Ad Hominem vs. Attack
- Why is it Often Claimed that Gods have a Gender?
- Why are basically all monotheistic religions ones that have a male god?
- Shifting through the Claims in support of Faith
- Dear Mr. AtHope, The 20th Century is an Indictment of Secularism and a Failed Atheist Century
- An Understanding of the Worldwide Statistics and Dynamics of Terrorist Incidents and Suicide Attacks
- Intoxication and Evolution? Addressing and Assessing the “Stoned Ape” or “Drunken Monkey” Theories as Catalysts in Human Evolution
- Sacred Menstrual cloth? Inanna’s knot, Isis knot, and maybe Ma’at’s feather?
- Damien, why don’t the Hebrews accept the bible stories?
- Dealing with a Troll and Arguing Over Word Meaning
- Knowledge without Belief? Justified beliefs or disbeliefs worthy of Knowledge?
- Afrocentrism and African Religions
- Crecganford @crecganford offers history & stories of the people, places, gods, & culture
- Empiricism-Denier?
I am not an academic. I am a revolutionary that teaches in public, in places like social media, and in the streets. I am not a leader by some title given but from my commanding leadership style of simply to start teaching everywhere to everyone, all manner of positive education.







ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref, ref
Low Gods “Earth” or Tutelary deity and High Gods “Sky” or Supreme deity
“An Earth goddess is a deification of the Earth. Earth goddesses are often associated with the “chthonic” deities of the underworld. Ki and Ninhursag are Mesopotamian earth goddesses. In Greek mythology, the Earth is personified as Gaia, corresponding to Roman Terra, Indic Prithvi/Bhūmi, etc. traced to an “Earth Mother” complementary to the “Sky Father” in Proto-Indo-European religion. Egyptian mythology exceptionally has a sky goddess and an Earth god.” ref
“A mother goddess is a goddess who represents or is a personification of nature, motherhood, fertility, creation, destruction or who embodies the bounty of the Earth. When equated with the Earth or the natural world, such goddesses are sometimes referred to as Mother Earth or as the Earth Mother. In some religious traditions or movements, Heavenly Mother (also referred to as Mother in Heaven or Sky Mother) is the wife or feminine counterpart of the Sky father or God the Father.” ref
“Any masculine sky god is often also king of the gods, taking the position of patriarch within a pantheon. Such king gods are collectively categorized as “sky father” deities, with a polarity between sky and earth often being expressed by pairing a “sky father” god with an “earth mother” goddess (pairings of a sky mother with an earth father are less frequent). A main sky goddess is often the queen of the gods and may be an air/sky goddess in her own right, though she usually has other functions as well with “sky” not being her main. In antiquity, several sky goddesses in ancient Egypt, Mesopotamia, and the Near East were called Queen of Heaven. Neopagans often apply it with impunity to sky goddesses from other regions who were never associated with the term historically. The sky often has important religious significance. Many religions, both polytheistic and monotheistic, have deities associated with the sky.” ref
“In comparative mythology, sky father is a term for a recurring concept in polytheistic religions of a sky god who is addressed as a “father”, often the father of a pantheon and is often either a reigning or former King of the Gods. The concept of “sky father” may also be taken to include Sun gods with similar characteristics, such as Ra. The concept is complementary to an “earth mother“. “Sky Father” is a direct translation of the Vedic Dyaus Pita, etymologically descended from the same Proto-Indo-European deity name as the Greek Zeûs Pater and Roman Jupiter and Germanic Týr, Tir or Tiwaz, all of which are reflexes of the same Proto-Indo-European deity’s name, *Dyēus Ph₂tḗr. While there are numerous parallels adduced from outside of Indo-European mythology, there are exceptions (e.g. In Egyptian mythology, Nut is the sky mother and Geb is the earth father).” ref
Tutelary deity
“A tutelary (also tutelar) is a deity or spirit who is a guardian, patron, or protector of a particular place, geographic feature, person, lineage, nation, culture, or occupation. The etymology of “tutelary” expresses the concept of safety and thus of guardianship. In late Greek and Roman religion, one type of tutelary deity, the genius, functions as the personal deity or daimon of an individual from birth to death. Another form of personal tutelary spirit is the familiar spirit of European folklore.” ref
“A tutelary (also tutelar) in Korean shamanism, jangseung and sotdae were placed at the edge of villages to frighten off demons. They were also worshiped as deities. Seonangshin is the patron deity of the village in Korean tradition and was believed to embody the Seonangdang. In Philippine animism, Diwata or Lambana are deities or spirits that inhabit sacred places like mountains and mounds and serve as guardians. Such as: Maria Makiling is the deity who guards Mt. Makiling and Maria Cacao and Maria Sinukuan. In Shinto, the spirits, or kami, which give life to human bodies come from nature and return to it after death. Ancestors are therefore themselves tutelaries to be worshiped. And similarly, Native American beliefs such as Tonás, tutelary animal spirit among the Zapotec and Totems, familial or clan spirits among the Ojibwe, can be animals.” ref
“A tutelary (also tutelar) in Austronesian beliefs such as: Atua (gods and spirits of the Polynesian peoples such as the Māori or the Hawaiians), Hanitu (Bunun of Taiwan‘s term for spirit), Hyang (Kawi, Sundanese, Javanese, and Balinese Supreme Being, in ancient Java and Bali mythology and this spiritual entity, can be either divine or ancestral), Kaitiaki (New Zealand Māori term used for the concept of guardianship, for the sky, the sea, and the land), Kawas (mythology) (divided into 6 groups: gods, ancestors, souls of the living, spirits of living things, spirits of lifeless objects, and ghosts), Tiki (Māori mythology, Tiki is the first man created by either Tūmatauenga or Tāne and represents deified ancestors found in most Polynesian cultures). ” ref, ref, ref, ref, ref, ref, ref
Mesopotamian Tutelary Deities can be seen as ones related to City-States
“Historical city-states included Sumerian cities such as Uruk and Ur; Ancient Egyptian city-states, such as Thebes and Memphis; the Phoenician cities (such as Tyre and Sidon); the five Philistine city-states; the Berber city-states of the Garamantes; the city-states of ancient Greece (the poleis such as Athens, Sparta, Thebes, and Corinth); the Roman Republic (which grew from a city-state into a vast empire); the Italian city-states from the Middle Ages to the early modern period, such as Florence, Siena, Ferrara, Milan (which as they grew in power began to dominate neighboring cities) and Genoa and Venice, which became powerful thalassocracies; the Mayan and other cultures of pre-Columbian Mesoamerica (including cities such as Chichen Itza, Tikal, Copán and Monte Albán); the central Asian cities along the Silk Road; the city-states of the Swahili coast; Ragusa; states of the medieval Russian lands such as Novgorod and Pskov; and many others.” ref
“The Uruk period (ca. 4000 to 3100 BCE; also known as Protoliterate period) of Mesopotamia, named after the Sumerian city of Uruk, this period saw the emergence of urban life in Mesopotamia and the Sumerian civilization. City-States like Uruk and others had a patron tutelary City Deity along with a Priest-King.” ref
“Chinese folk religion, both past, and present, includes myriad tutelary deities. Exceptional individuals, highly cultivated sages, and prominent ancestors can be deified and honored after death. Lord Guan is the patron of military personnel and police, while Mazu is the patron of fishermen and sailors. Such as Tu Di Gong (Earth Deity) is the tutelary deity of a locality, and each individual locality has its own Earth Deity and Cheng Huang Gong (City God) is the guardian deity of an individual city, worshipped by local officials and locals since imperial times.” ref
“A tutelary (also tutelar) in Hinduism, personal tutelary deities are known as ishta-devata, while family tutelary deities are known as Kuladevata. Gramadevata are guardian deities of villages. Devas can also be seen as tutelary. Shiva is the patron of yogis and renunciants. City goddesses include: Mumbadevi (Mumbai), Sachchika (Osian); Kuladevis include: Ambika (Porwad), and Mahalakshmi. In NorthEast India Meitei mythology and religion (Sanamahism) of Manipur, there are various types of tutelary deities, among which Lam Lais are the most predominant ones. Tibetan Buddhism has Yidam as a tutelary deity. Dakini is the patron of those who seek knowledge.” ref
“A tutelary (also tutelar) The Greeks also thought deities guarded specific places: for instance, Athena was the patron goddess of the city of Athens. Socrates spoke of hearing the voice of his personal spirit or daimonion:
You have often heard me speak of an oracle or sign which comes to me … . This sign I have had ever since I was a child. The sign is a voice which comes to me and always forbids me to do something which I am going to do, but never commands me to do anything, and this is what stands in the way of my being a politician.” ref
“Tutelary deities who guard and preserve a place or a person are fundamental to ancient Roman religion. The tutelary deity of a man was his Genius, that of a woman her Juno. In the Imperial era, the Genius of the Emperor was a focus of Imperial cult. An emperor might also adopt a major deity as his personal patron or tutelary, as Augustus did Apollo. Precedents for claiming the personal protection of a deity were established in the Republican era, when for instance the Roman dictator Sulla advertised the goddess Victory as his tutelary by holding public games (ludi) in her honor.” ref
“Each town or city had one or more tutelary deities, whose protection was considered particularly vital in time of war and siege. Rome itself was protected by a goddess whose name was to be kept ritually secret on pain of death (for a supposed case, see Quintus Valerius Soranus). The Capitoline Triad of Juno, Jupiter, and Minerva were also tutelaries of Rome. The Italic towns had their own tutelary deities. Juno often had this function, as at the Latin town of Lanuvium and the Etruscan city of Veii, and was often housed in an especially grand temple on the arx (citadel) or other prominent or central location. The tutelary deity of Praeneste was Fortuna, whose oracle was renowned.” ref
“The Roman ritual of evocatio was premised on the belief that a town could be made vulnerable to military defeat if the power of its tutelary deity were diverted outside the city, perhaps by the offer of superior cult at Rome. The depiction of some goddesses such as the Magna Mater (Great Mother, or Cybele) as “tower-crowned” represents their capacity to preserve the city. A town in the provinces might adopt a deity from within the Roman religious sphere to serve as its guardian, or syncretize its own tutelary with such; for instance, a community within the civitas of the Remi in Gaul adopted Apollo as its tutelary, and at the capital of the Remi (present-day Rheims), the tutelary was Mars Camulus.” ref
Household deity (a kind of or related to a Tutelary deity)
“A household deity is a deity or spirit that protects the home, looking after the entire household or certain key members. It has been a common belief in paganism as well as in folklore across many parts of the world. Household deities fit into two types; firstly, a specific deity – typically a goddess – often referred to as a hearth goddess or domestic goddess who is associated with the home and hearth, such as the ancient Greek Hestia.” ref
“The second type of household deities are those that are not one singular deity, but a type, or species of animistic deity, who usually have lesser powers than major deities. This type was common in the religions of antiquity, such as the Lares of ancient Roman religion, the Gashin of Korean shamanism, and Cofgodas of Anglo-Saxon paganism. These survived Christianisation as fairy-like creatures existing in folklore, such as the Anglo-Scottish Brownie and Slavic Domovoy.” ref
“Household deities were usually worshipped not in temples but in the home, where they would be represented by small idols (such as the teraphim of the Bible, often translated as “household gods” in Genesis 31:19 for example), amulets, paintings, or reliefs. They could also be found on domestic objects, such as cosmetic articles in the case of Tawaret. The more prosperous houses might have a small shrine to the household god(s); the lararium served this purpose in the case of the Romans. The gods would be treated as members of the family and invited to join in meals, or be given offerings of food and drink.” ref
“In many religions, both ancient and modern, a god would preside over the home. Certain species, or types, of household deities, existed. An example of this was the Roman Lares. Many European cultures retained house spirits into the modern period. Some examples of these include:
- Brownie (Scotland and England) or Hob (England) / Kobold (Germany) / Goblin / Hobgoblin
- Domovoy (Slavic)
- Nisse (Norwegian or Danish) / Tomte (Swedish) / Tonttu (Finnish)
- Húsvættir (Norse)” ref
“Although the cosmic status of household deities was not as lofty as that of the Twelve Olympians or the Aesir, they were also jealous of their dignity and also had to be appeased with shrines and offerings, however humble. Because of their immediacy they had arguably more influence on the day-to-day affairs of men than the remote gods did. Vestiges of their worship persisted long after Christianity and other major religions extirpated nearly every trace of the major pagan pantheons. Elements of the practice can be seen even today, with Christian accretions, where statues to various saints (such as St. Francis) protect gardens and grottos. Even the gargoyles found on older churches, could be viewed as guardians partitioning a sacred space.” ref
“For centuries, Christianity fought a mop-up war against these lingering minor pagan deities, but they proved tenacious. For example, Martin Luther‘s Tischreden have numerous – quite serious – references to dealing with kobolds. Eventually, rationalism and the Industrial Revolution threatened to erase most of these minor deities, until the advent of romantic nationalism rehabilitated them and embellished them into objects of literary curiosity in the 19th century. Since the 20th century this literature has been mined for characters for role-playing games, video games, and other fantasy personae, not infrequently invested with invented traits and hierarchies somewhat different from their mythological and folkloric roots.” ref
“In contradistinction to both Herbert Spencer and Edward Burnett Tylor, who defended theories of animistic origins of ancestor worship, Émile Durkheim saw its origin in totemism. In reality, this distinction is somewhat academic, since totemism may be regarded as a particularized manifestation of animism, and something of a synthesis of the two positions was attempted by Sigmund Freud. In Freud’s Totem and Taboo, both totem and taboo are outward expressions or manifestations of the same psychological tendency, a concept which is complementary to, or which rather reconciles, the apparent conflict. Freud preferred to emphasize the psychoanalytic implications of the reification of metaphysical forces, but with particular emphasis on its familial nature. This emphasis underscores, rather than weakens, the ancestral component.” ref
“William Edward Hearn, a noted classicist, and jurist, traced the origin of domestic deities from the earliest stages as an expression of animism, a belief system thought to have existed also in the neolithic, and the forerunner of Indo-European religion. In his analysis of the Indo-European household, in Chapter II “The House Spirit”, Section 1, he states:
The belief which guided the conduct of our forefathers was … the spirit rule of dead ancestors.” ref
“In Section 2 he proceeds to elaborate:
It is thus certain that the worship of deceased ancestors is a vera causa, and not a mere hypothesis. …
In the other European nations, the Slavs, the Teutons, and the Kelts, the House Spirit appears with no less distinctness. … [T]he existence of that worship does not admit of doubt. … The House Spirits had a multitude of other names which it is needless here to enumerate, but all of which are more or less expressive of their friendly relations with man. … In [England] … [h]e is the Brownie. … In Scotland this same Brownie is well known. He is usually described as attached to particular families, with whom he has been known to reside for centuries, threshing the corn, cleaning the house, and performing similar household tasks. His favorite gratification was milk and honey.” ref

Hinduism around 3,700 to 3,500 years old. ref
Judaism around 3,450 or 3,250 years old. (The first writing in the bible was “Paleo-Hebrew” dated to around 3,000 years ago Khirbet Qeiyafa is the site of an ancient fortress city overlooking the Elah Valley. And many believe the religious Jewish texts were completed around 2,500) ref, ref
Judaism is around 3,450 or 3,250 years old. (“Paleo-Hebrew” 3,000 years ago and Torah 2,500 years ago)
“Judaism is an Abrahamic, its roots as an organized religion in the Middle East during the Bronze Age. Some scholars argue that modern Judaism evolved from Yahwism, the religion of ancient Israel and Judah, by the late 6th century BCE, and is thus considered to be one of the oldest monotheistic religions.” ref
“Yahwism is the name given by modern scholars to the religion of ancient Israel, essentially polytheistic, with a plethora of gods and goddesses. Heading the pantheon was Yahweh, the national god of the Israelite kingdoms of Israel and Judah, with his consort, the goddess Asherah; below them were second-tier gods and goddesses such as Baal, Shamash, Yarikh, Mot, and Astarte, all of whom had their own priests and prophets and numbered royalty among their devotees, and a third and fourth tier of minor divine beings, including the mal’ak, the messengers of the higher gods, who in later times became the angels of Judaism, Christianity and Islam. Yahweh, however, was not the ‘original’ god of Israel “Isra-El”; it is El, the head of the Canaanite pantheon, whose name forms the basis of the name “Israel”, and none of the Old Testament patriarchs, the tribes of Israel, the Judges, or the earliest monarchs, have a Yahwistic theophoric name (i.e., one incorporating the name of Yahweh).” ref
“El is a Northwest Semitic word meaning “god” or “deity“, or referring (as a proper name) to any one of multiple major ancient Near Eastern deities. A rarer form, ‘ila, represents the predicate form in Old Akkadian and in Amorite. The word is derived from the Proto-Semitic *ʔil-, meaning “god”. Specific deities known as ‘El or ‘Il include the supreme god of the ancient Canaanite religion and the supreme god of East Semitic speakers in Mesopotamia’s Early Dynastic Period. ʼĒl is listed at the head of many pantheons. In some Canaanite and Ugaritic sources, ʼĒl played a role as father of the gods, of creation, or both. For example, in the Ugaritic texts, ʾil mlk is understood to mean “ʼĒl the King” but ʾil hd as “the god Hadad“. The Semitic root ʾlh (Arabic ʾilāh, Aramaic ʾAlāh, ʾElāh, Hebrew ʾelōah) may be ʾl with a parasitic h, and ʾl may be an abbreviated form of ʾlh. In Ugaritic the plural form meaning “gods” is ʾilhm, equivalent to Hebrew ʾelōhîm “powers”. In the Hebrew texts this word is interpreted as being semantically singular for “god” by biblical commentators. However the documentary hypothesis for the Old Testament (corresponds to the Jewish Torah) developed originally in the 1870s, identifies these that different authors – the Jahwist, Elohist, Deuteronomist, and the Priestly source – were responsible for editing stories from a polytheistic religion into those of a monotheistic religion. Inconsistencies that arise between monotheism and polytheism in the texts are reflective of this hypothesis.” ref
Jainism around 2,599 – 2,527 years old. ref
Confucianism around 2,600 – 2,551 years old. ref
Buddhism around 2,563/2,480 – 2,483/2,400 years old. ref
Christianity around 2,o00 years old. ref
Shinto around 1,305 years old. ref
Islam around 1407–1385 years old. ref

Knowledge to Ponder:
Stars/Astrology:
- Possibly, around 30,000 years ago (in simpler form) to 6,000 years ago, Stars/Astrology are connected to Ancestors, Spirit Animals, and Deities.
- The star also seems to be a possible proto-star for Star of Ishtar, Star of Inanna, or Star of Venus.
- Around 7,000 to 6,000 years ago, Star Constellations/Astrology have connections to the “Kurgan phenomenon” of below-ground “mound” stone/wood burial structures and “Dolmen phenomenon” of above-ground stone burial structures.
- Around 6,500–5,800 years ago, The Northern Levant migrations into Jordon and Israel in the Southern Levant brought new cultural and religious transfer from Turkey and Iran.
- “The Ghassulian Star,” a mysterious 6,000-year-old mural from Jordan may have connections to the European paganstic kurgan/dolmens phenomenon.
“Astrology is a range of divinatory practices, recognized as pseudoscientific since the 18th century, that claim to discern information about human affairs and terrestrial events by studying the apparent positions of celestial objects. Different cultures have employed forms of astrology since at least the 2nd millennium BCE, these practices having originated in calendrical systems used to predict seasonal shifts and to interpret celestial cycles as signs of divine communications. Most, if not all, cultures have attached importance to what they observed in the sky, and some—such as the Hindus, Chinese, and the Maya—developed elaborate systems for predicting terrestrial events from celestial observations. Western astrology, one of the oldest astrological systems still in use, can trace its roots to 19th–17th century BCE Mesopotamia, from where it spread to Ancient Greece, Rome, the Islamicate world and eventually Central and Western Europe. Contemporary Western astrology is often associated with systems of horoscopes that purport to explain aspects of a person’s personality and predict significant events in their lives based on the positions of celestial objects; the majority of professional astrologers rely on such systems.” ref
Around 5,500 years ago, Science evolves, The first evidence of science was 5,500 years ago and was demonstrated by a body of empirical, theoretical, and practical knowledge about the natural world. ref
Around 5,000 years ago, Origin of Logics is a Naturalistic Observation (principles of valid reasoning, inference, & demonstration) ref
Around 4,150 to 4,000 years ago: The earliest surviving versions of the Sumerian Epic of Gilgamesh, which was originally titled “He who Saw the Deep” (Sha naqba īmuru) or “Surpassing All Other Kings” (Shūtur eli sharrī) were written. ref
Hinduism:
- 3,700 years ago or so, the oldest of the Hindu Vedas (scriptures), the Rig Veda was composed.
- 3,500 years ago or so, the Vedic Age began in India after the collapse of the Indus Valley Civilization.
Judaism:
- around 3,000 years ago, the first writing in the bible was “Paleo-Hebrew”
- around 2,500 years ago, many believe the religious Jewish texts were completed
Myths: The bible inspired religion is not just one religion or one myth but a grouping of several religions and myths
- Around 3,450 or 3,250 years ago, according to legend, is the traditionally accepted period in which the Israelite lawgiver, Moses, provided the Ten Commandments.
- Around 2,500 to 2,400 years ago, a collection of ancient religious writings by the Israelites based primarily upon the Hebrew Bible, Tanakh, or Old Testament is the first part of Christianity’s bible.
- Around 2,400 years ago, the most accepted hypothesis is that the canon was formed in stages, first the Pentateuch (Torah).
- Around 2,140 to 2,116 years ago, the Prophets was written during the Hasmonean dynasty, and finally the remaining books.
- Christians traditionally divide the Old Testament into four sections:
- The first five books or Pentateuch (Torah).
- The proposed history books telling the history of the Israelites from their conquest of Canaan to their defeat and exile in Babylon.
- The poetic and proposed “Wisdom books” dealing, in various forms, with questions of good and evil in the world.
- The books of the biblical prophets, warning of the consequences of turning away from God:
- Henotheism:
- Exodus 20:23 “You shall not make other gods besides Me (not saying there are no other gods just not to worship them); gods of silver or gods of gold, you shall not make for yourselves.”
- Polytheism:
- Judges 10:6 “Then the sons of Israel again did evil in the sight of the LORD, served the Baals and the Ashtaroth, the gods of Aram, the gods of Sidon, the gods of Moab, the gods of the sons of Ammon, and the gods of the Philistines; thus they forsook the LORD and did not serve Him.”
- 1 Corinthians 8:5 “For even if there are so-called gods whether in heaven or on earth, as indeed there are many gods and many lords.”
- Monotheism:
- Isaiah 43:10 “You are my witnesses,” declares the LORD, “and my servant whom I have chosen, so that you may know and believe me and understand that I am he. Before me no god was formed, nor will there be one after me.
Around 2,570 to 2,270 Years Ago, there is a confirmation of atheistic doubting as well as atheistic thinking, mainly by Greek philosophers. However, doubting gods is likely as old as the invention of gods and should destroy the thinking that belief in god(s) is the “default belief”. The Greek word is apistos (a “not” and pistos “faithful,”), thus not faithful or faithless because one is unpersuaded and unconvinced by a god(s) claim. Short Definition: unbelieving, unbeliever, or unbelief.

Expressions of Atheistic Thinking:
- Around 2,600 years ago, Ajita Kesakambali, ancient Indian philosopher, who is the first known proponent of Indian materialism. ref
- Around 2,535 to 2,475 years ago, Heraclitus, Greek pre-Socratic philosopher, a native of the Greek city Ephesus, Ionia, on the coast of Anatolia, also known as Asia Minor or modern Turkey. ref
- Around 2,500 to 2,400 years ago, according to The Story of Civilization book series certain African pygmy tribes have no identifiable gods, spirits, or religious beliefs or rituals, and even what burials accrue are without ceremony. ref
- Around 2,490 to 2,430 years ago, Empedocles, Greek pre-Socratic philosopher and a citizen of Agrigentum, a Greek city in Sicily. ref
- Around 2,460 to 2,370 years ago, Democritus, Greek pre-Socratic philosopher considered to be the “father of modern science” possibly had some disbelief amounting to atheism. ref
- Around 2,399 years ago or so, Socrates, a famous Greek philosopher was tried for sinfulness by teaching doubt of state gods. ref
- Around 2,341 to 2,270 years ago, Epicurus, a Greek philosopher known for composing atheistic critics and famously stated, “Is God willing to prevent evil, but not able? Then he is not omnipotent. Is he able, but not willing? Then he is malevolent. Is he both able and willing? Then whence cometh evil? Is he neither able nor willing? Then why call him god?” ref
This last expression by Epicurus, seems to be an expression of Axiological Atheism. To understand and utilize value or actually possess “Value Conscious/Consciousness” to both give a strong moral “axiological” argument (the problem of evil) as well as use it to fortify humanism and positive ethical persuasion of human helping and care responsibilities. Because value-blindness gives rise to sociopathic/psychopathic evil.



While hallucinogens are associated with shamanism, it is alcohol that is associated with paganism.
The Atheist-Humanist-Leftist Revolutionaries Shows in the prehistory series:
Show two: Pre-animism 300,000 years old and animism 100,000 years old: related to “Anarchism and Socialism”
Show tree: Totemism 50,000 years old: related to “Anarchism and Socialism”
Show four: Shamanism 30,000 years old: related to “Anarchism and Socialism”
Show five: Paganism 12,000 years old: related to “Anarchism and Socialism”
Show six: Emergence of hierarchy, sexism, slavery, and the new male god dominance: Paganism 7,000-5,000 years old: related to “Anarchism and Socialism” (Capitalism) (World War 0) Elite and their slaves!
Prehistory: related to “Anarchism and Socialism” the division of labor, power, rights, and recourses: VIDEO
Pre-animism 300,000 years old and animism 100,000 years old: related to “Anarchism and Socialism”: VIDEO
Totemism 50,000 years old: related to “Anarchism and Socialism”: VIDEO
Shamanism 30,000 years old: related to “Anarchism and Socialism”: VIDEO
Paganism 12,000 years old: related to “Anarchism and Socialism” (Pre-Capitalism): VIDEO
Paganism 7,000-5,000 years old: related to “Anarchism and Socialism” (Capitalism) (World War 0) Elite and their slaves: VIEDO
Paganism 5,000 years old: progressed organized religion and the state: related to “Anarchism and Socialism” (Kings and the Rise of the State): VIEDO
Paganism 4,000 years old: related to “Anarchism and Socialism” (First Moralistic gods, then the Origin time of Monotheism): VIEDO
I do not hate simply because I challenge and expose myths or lies any more than others being thought of as loving simply because of the protection and hiding from challenge their favored myths or lies.
The truth is best championed in the sunlight of challenge.
An archaeologist once said to me “Damien religion and culture are very different”
My response, So are you saying that was always that way, such as would you say Native Americans’ cultures are separate from their religions? And do you think it always was the way you believe?
I had said that religion was a cultural product. That is still how I see it and there are other archaeologists that think close to me as well. Gods too are the myths of cultures that did not understand science or the world around them, seeing magic/supernatural everywhere.
I personally think there is a goddess and not enough evidence to support a male god at Çatalhöyük but if there was both a male and female god and goddess then I know the kind of gods they were like Proto-Indo-European mythology.
This series idea was addressed in, Anarchist Teaching as Free Public Education or Free Education in the Public: VIDEO
Our 12 video series: Organized Oppression: Mesopotamian State Force and the Politics of power (9,000-4,000 years ago), is adapted from: The Complete and Concise History of the Sumerians and Early Bronze Age Mesopotamia (7000-2000 BC): https://www.youtube.com/watch?v=szFjxmY7jQA by “History with Cy“
Show #1: Mesopotamian State Force and the Politics of Power (Samarra, Halaf, Ubaid)
Show #2: Mesopotamian State Force and the Politics of Power
Show #3: Mesopotamian State Force and the Politics of Power (Uruk and the First Cities)
Show #4: Mesopotamian State Force and the Politics of Power (First Kings)
Show #5: Mesopotamian State Force and the Politics of Power (Early Dynastic Period)
Show #6: Mesopotamian State Force and the Politics of Power
Show #7: Mesopotamian State Force and the Politics of Power (Sargon and Akkadian Rule)
Show #9: Mesopotamian State Force and the Politics of Power (Gudea of Lagash and Utu-hegal)
Show #12: Mesopotamian State Force and the Politics of Power (Aftermath and Legacy of Sumer)

The “Atheist-Humanist-Leftist Revolutionaries”
Cory Johnston ☭ Ⓐ Atheist Leftist @Skepticallefty & I (Damien Marie AtHope) @AthopeMarie (my YouTube & related blog) are working jointly in atheist, antitheist, antireligionist, antifascist, anarchist, socialist, and humanist endeavors in our videos together, generally, every other Saturday.
Why Does Power Bring Responsibility?
Think, how often is it the powerless that start wars, oppress others, or commit genocide? So, I guess the question is to us all, to ask, how can power not carry responsibility in a humanity concept? I know I see the deep ethical responsibility that if there is power their must be a humanistic responsibility of ethical and empathic stewardship of that power. Will I be brave enough to be kind? Will I possess enough courage to be compassionate? Will my valor reach its height of empathy? I as everyone, earns our justified respect by our actions, that are good, ethical, just, protecting, and kind. Do I have enough self-respect to put my love for humanity’s flushing, over being brought down by some of its bad actors? May we all be the ones doing good actions in the world, to help human flourishing.
I create the world I want to live in, striving for flourishing. Which is not a place but a positive potential involvement and promotion; a life of humanist goal precision. To master oneself, also means mastering positive prosocial behaviors needed for human flourishing. I may have lost a god myth as an atheist, but I am happy to tell you, my friend, it is exactly because of that, leaving the mental terrorizer, god belief, that I truly regained my connected ethical as well as kind humanity.
Cory and I will talk about prehistory and theism, addressing the relevance to atheism, anarchism, and socialism.
At the same time as the rise of the male god, 7,000 years ago, there was also the very time there was the rise of violence, war, and clans to kingdoms, then empires, then states. It is all connected back to 7,000 years ago, and it moved across the world.
Cory Johnston: https://damienmarieathope.com/2021/04/cory-johnston-mind-of-a-skeptical-leftist/?v=32aec8db952d
The Mind of a Skeptical Leftist (YouTube)
Cory Johnston: Mind of a Skeptical Leftist @Skepticallefty
The Mind of a Skeptical Leftist By Cory Johnston: “Promoting critical thinking, social justice, and left-wing politics by covering current events and talking to a variety of people. Cory Johnston has been thoughtfully talking to people and attempting to promote critical thinking, social justice, and left-wing politics.” http://anchor.fm/skepticalleft
Cory needs our support. We rise by helping each other.
Cory Johnston ☭ Ⓐ @Skepticallefty Evidence-based atheist leftist (he/him) Producer, host, and co-host of 4 podcasts @skeptarchy @skpoliticspod and @AthopeMarie
Damien Marie AtHope (“At Hope”) Axiological Atheist, Anti-theist, Anti-religionist, Secular Humanist. Rationalist, Writer, Artist, Poet, Philosopher, Advocate, Activist, Psychology, and Armchair Archaeology/Anthropology/Historian.
Damien is interested in: Freedom, Liberty, Justice, Equality, Ethics, Humanism, Science, Atheism, Antiteism, Antireligionism, Ignosticism, Left-Libertarianism, Anarchism, Socialism, Mutualism, Axiology, Metaphysics, LGBTQI, Philosophy, Advocacy, Activism, Mental Health, Psychology, Archaeology, Social Work, Sexual Rights, Marriage Rights, Woman’s Rights, Gender Rights, Child Rights, Secular Rights, Race Equality, Ageism/Disability Equality, Etc. And a far-leftist, “Anarcho-Humanist.”
I am not a good fit in the atheist movement that is mostly pro-capitalist, I am anti-capitalist. Mostly pro-skeptic, I am a rationalist not valuing skepticism. Mostly pro-agnostic, I am anti-agnostic. Mostly limited to anti-Abrahamic religions, I am an anti-religionist.
To me, the “male god” seems to have either emerged or become prominent around 7,000 years ago, whereas the now favored monotheism “male god” is more like 4,000 years ago or so. To me, the “female goddess” seems to have either emerged or become prominent around 11,000-10,000 years ago or so, losing the majority of its once prominence around 2,000 years ago due largely to the now favored monotheism “male god” that grow in prominence after 4,000 years ago or so.
My Thought on the Evolution of Gods?
Animal protector deities from old totems/spirit animal beliefs come first to me, 13,000/12,000 years ago, then women as deities 11,000/10,000 years ago, then male gods around 7,000/8,000 years ago. Moralistic gods around 5,000/4,000 years ago, and monotheistic gods around 4,000/3,000 years ago.

Damien Marie AtHope (Said as “At” “Hope”)/(Autodidact Polymath but not good at math):
Axiological Atheist, Anti-theist, Anti-religionist, Secular Humanist, Rationalist, Writer, Artist, Jeweler, Poet, “autodidact” Philosopher, schooled in Psychology, and “autodidact” Armchair Archaeology/Anthropology/Pre-Historian (Knowledgeable in the range of: 1 million to 5,000/4,000 years ago). I am an anarchist socialist politically. Reasons for or Types of Atheism
My Website, My Blog, & Short-writing or Quotes, My YouTube, Twitter: @AthopeMarie, and My Email: damien.marie.athope@gmail.com



