Justifying Judgments: Possibility and Epistemic Utility theory
The Rationalist Desire for Epistemically Credible Thinking
As a rationalist when I debate or challenge a position or thinking I want the epistemically provable truth, as I am not only closed to my own ideas, rather, I am just as will to adapt my position if given strong warrant or justification supported by valid and reliable reason and evidence with epistemic credibility.
Normative Theories of Rational Choice: Expected Utility
Rational Choice in a Normative Theory of Expected Utility = Utility (the axiology: value, goodness, credibility, accuracy, worth or usefulness) Theory.
“a theory of how people should rationally make decisions”
According to Rachael Briggs at The Stanford Encyclopedia of Philosophy, the expected utility of an act is a weighted average of the utilities of each of its possible outcomes, where the utility of an outcome measures the extent to which that outcome is preferred, or preferable, to the alternatives. The utility of each outcome is weighted according to the probability that the act will lead to that outcome. A basic definition of expected utility should involve epistemically rigorous process in general, and discuss its relationship to choice. Utility (axiology worth/usefulness) Theory can address two main types of arguments for expected utility: representation theorems, and long-run statistical arguments with (axiology worth/usefulness) applications in philosophy of religion, economics, ethics, and epistemology. Why choose acts that maximize expected utility? One possible answer is that expected utility theory is rational bedrock—that means-end rationality essentially involves maximizing expected utility. For those who find this answer unsatisfying, however, there are two further sources of justification. First, there are long-run arguments, which rely on evidence that expected-utility maximization is a profitable policy in the long term. Second, there are arguments based on representation theorems, which suggest that certain rational constraints on preference entail that all rational agents maximize expected utility. Mathematical proofs of Representability are called representation theorems, representation theorems, where the formulation of this argument—slightly modified to reflect the role of utilities as well as probabilities. RefThe expected utility argument has three premises, The Rationality Condition, The Axiom Preference, & Representability
- The Rationality Condition: If a person can be represented as having degrees of belief that obey the probability calculus [and a utility function such that she prefers acts with higher expected utility], then the person really has degrees of belief that obey the laws of the probability calculus [and really does prefer acts with higher expected utility]. Ref
- The Axiom Preference: The axioms of expected utility theory are the axioms of rational preference. If a person’s preferences obey the axioms of expected utility theory, then the user can be represented as having degrees of belief that obey the laws of the probability calculus [and a utility function such that the user prefers acts with higher expected utility]. And if a person [fails to prefer acts with higher expected utility], then that person violates at least one of the axioms of rational preference. Therefore, if the premises are true, the argument shows that there is something wrong with people whose preferences are at odds with expected utility theory—they violate the axioms of rational preference. Ref
- Representability: Mathematical proofs of representability are called representation theorems which may rely on different set(s) of axioms. No matter which set of axioms we use, the Rationality and or Reality Conditions are controversial. In some cases, preferences that seem rationally permissible—perhaps even rationally required—violate the axioms of expected utility theory. The Reality Condition to be representable using a probability and utility function is not to have a probability and utility function. After all, an agent who can be represented as an expected utility maximizer with degrees of belief that obey the probability calculus, can also be represented as someone who fails to maximize expected utility with degrees of belief that violate the probability calculus. Why think the expected utility representation is the right one? There are several options. Perhaps the defender of representation theorems can stipulate that what it is to have particular degrees of belief and utilities is just to have the corresponding preferences. The main challenge for defenders of this response is to explain why representations in terms of expected utility are explanatorily useful, and why they are better than alternative representations. Or perhaps probabilities and utilities are a good cleaned-up theoretical substitutes for our folk notions of belief and desire—precise scientific substitutes for our folk concepts. Although, probabilities and utilities can be poor stand-ins for our folk notions. A third possibility, is that facts about degrees of belief are made true independently of the agent’s preferences, and provide a principled way to restrict the range of acceptable representations. The challenge for defenders of this type of response is to specify what these additional facts are. Ref
Four Passable Applications: Epistemology, Ethics, Economics, & Religion/gods
- Epistemology Applications for Utility Theory: Expected utility theory can be used to address practical questions in epistemology. One such question is when to accept a hypothesis. In typical cases, the evidence is logically compatible with multiple hypotheses, including hypotheses to which it lends little inductive support. Furthermore, scientists do not typically accept only those hypotheses that are most probable given their data. When is a hypothesis likely enough to deserve acceptance? Bayesians, may suggest that this decision be made on expected utility grounds. Whether to accept a hypothesis is a decision problem, with acceptance and rejection as acts. Ref
- Ethics Applications for Utility Theory: Consequentialists hold that the rightness or wrongness of an act is determined by the moral goodness or badness of its consequences, possibly meant as we ought to do whatever will in fact have the best consequences. But it is difficult to know with any degree of certainty what long-term consequences our acts will have. It could be argued that in some cases, we cannot act to bring about the best consequences simply because we do not or may not know how. (Similarly, I cannot beat a chess master, since I do not know how—even though there is a sequence of moves I can perform that would constitute beating a chess master at chess.) Since “ought” implies “can”, it must be false in some cases that we ought to act to bring about the best consequences and even if we can perform the acts with the best consequences, the view that we ought to do so still could yields strange consequences: even the morally best people can and or do act immorally some of the time. Alternatively, the possible right act is the one with the greatest expected moral value, not the one that will in fact always yield the best consequences. It may be highlighted how the expected moral value of an act depends on which probability function we work with. Therefore, while every probability function is associated with an “ought”, the “ought” that matters most to action is the one associated with the decision-maker’s degrees of belief at the time of action. Other authors claim priority for other “oughts”; or one could favor the probability function that is most reasonable for the agent to adopt in response to her evidence, given her epistemic limitations; or one could favor the objective chance function as a measure of objective rightness. (They appeal to a more complicated probability function to define a notion of “subjective rightness” for decisionmakers who are ignorant of the objective chances.) Still other options could argue that even if that we ought to do whatever will have the best consequences, expected utility theory can play the role of a decision procedure when we are uncertain what consequences our acts will have. However, its applied or reasoned objects that expected utility calculations are horribly impractical. In most real-life decisions, the steps required to compute expected utilities are beyond our ken: listing the possible outcomes of our acts, assigning each outcome a utility and a conditional probability given each act, and performing the arithmetic necessary to expected utility calculations. Ref
- Economics Question Applications for Utility Theory: In economics, expected utility theory is often invoked as an account of how people actually make decisions in an economic context. These uses of expected utility theory are descriptive, and don’t bear directly on the normative question of whether expected utility theory provides a good account of rationality. Ref
- Religion or god Question Applications for Utility Theory: One of the earliest (but highly flawed) applications of expected utility theory in Pascal’s wager, an argument for the conclusion belief in god is rationally obligatory (which it does nothing of the kind as it’s a black or white when it’s a color world with a full range of colored possibilities; intentionally or unintendedly excluded making it highly flawed). In Pascal’s assessment, participation in this wager is not optional. Merely by existing in a state of uncertainty, we are forced to choose between the available courses of action for practical purposes. Pascal presents a number of distinct arguments, but one particularly notable version relies on expected utility considerations. Pascal arguments expected utility considerations would report that because we lack decisive evidence about whether a god (it only considers the christian bible god only) exists. However, the question of whether to believe in Pascal arguments for this black or white christian bible “only” considered option (even though there are thousands of god myths) can be understood as a decision problem, in which belief and disbelief are both acts. Pascal argues that belief in god is the better act: “there is here an infinity of an infinitely happy life to gain, a chance of gain against a finite number of chances of loss, and what you stake is finite.” This looks like an argument based on expected utility theory but has an unjustified limited choice which its self could involve a justified use of utility theory, such as the question as to when to accept a hypothesis Pascal arguments for this black or white christian bible “only” epistemologically considered option. In typical cases, the evidence is logically compatible with multiple hypotheses, including hypotheses to which it lends little inductive support. Ref
More Criticism of Pascal’s Wager
According to Wikimedia, Criticism of Pascal’s Wager began in his own day, and came from both atheists, who questioned the ‘benefits’ of a deity whose ‘realm’ is beyond reason, and the religiously orthodox, who primarily took issue with the wager’s deistic and agnostic language. It is criticized for not proving God’s existence, the encouragement of false belief, and the problem of which religion and which God should be worshipped. refNature as not a proof of the existence of a god
Voltaire (another prominent French writer of the Enlightenment), a generation after Pascal, rejected the idea that the wager was “proof of God” as “indecent and childish”, adding, “the interest I have to believe a thing is no proof that such a thing exists”. Pascal, however, did not advance the wager as a proof of gOD’s existence but rather as a necessary pragmatic decision which is “impossible to avoid” for any living person. He argued that abstaining from making a wager is not an option and that “reason is incapable of divining the truth”; thus, a decision of whether or not to believe in the existence of gOD must be made by “considering the consequences of each possibility”. Voltaire’s critique concerns not the nature of the Pascalian wager as proof of gOD’s existence, but the contention that the very belief Pascal tried to promote is not convincing. Voltaire hints at the fact that Pascal, as a Jansenist, believed that only a small, and already predestined, portion of humanity would eventually be saved by gOD. Voltaire explained that no matter how far someone is tempted with rewards to believe in Christian salvation, the result will be at best a faint belief. Pascal, in his Pensees, agrees with this, not stating that people can choose to believe (and therefore make a safe wager), but rather that some cannot believe. As Étienne Souriau explained, in order to accept Pascal’s argument, the bettor needs to be certain that God seriously intends to honour the bet; he says that the Wager assumes that God also accepts the bet, which is not proved; Pascal’s bettor is here like the fool who seeing a leaf floating on a river’s waters and quivering at some point, for a few seconds, between the two sides of a stone, says: “I bet a million with Rothschild that it takes finally the left path.” And, effectively, the leaf passed on the left side of the stone, but unfortunately for the fool Rothschild never said “I [will take that] bet”. refArgument from inconsistent revelations
Since there have been many religions throughout history, and therefore many conceptions of gOD (or gods), some assert that all of them need to be factored into the Wager, in an argument known as the argument from inconsistent revelations. This, its proponents argue, would lead to a high probability of believing in “the wrong god”, which, they claim, eliminates the mathematical advantage Pascal claimed with his Wager. Denis Diderot, a contemporary of Voltaire, concisely expressed this opinion when asked about the Wager, saying “an Imam could reason the same way”. J. L. Mackie notes that “the church within which alone salvation is to be found is not necessarily the Church of Rome, but perhaps that of the Anabaptists or members of The Church of Jesus Christ of Latter-day Saints or the Muslim Sunnis or the worshipers of Kali or of Odin.” Another version of this objection argues that for every religion that promulgates rules, there exists another religion that has rules of the opposite kind. If a certain action leads one closer to salvation in the former religion, it leads one further away from it in the latter. Therefore, the expected value of following a certain religion could be negative. Or, one could also argue that there are an infinite number of mutually exclusive religions (which is a subset of the set of all possible religions), and that the probability of any one of them being true is zero; therefore, the expected value of following a certain religion is zero. Pascal considers this type of objection briefly in the notes compiled into the Pensées, and dismisses it as obviously wrong and disingenuous: What say [the unbelievers] then? “Do we not see,” say they, “that the brutes live and die like men, and Turks like Christians? They have their ceremonies, their prophets, their doctors, their saints, their monks, like us,” etc. If you care but little to know the truth, that is enough to leave you in repose. But if you desire with all your heart to know it, it is not enough; look at it in detail. That would be sufficient for a question in philosophy; but not here, where everything is at stake. And yet, after a superficial reflection of this kind, we go to amuse ourselves, etc. Let us inquire of this same religion whether it does not give a reason for this obscurity; perhaps it will teach it to us. This short but densely packed passage, which alludes to numerous themes discussed elsewhere in the Pensées, has given rise to many pages of scholarly analysis. Pascal says that unbelievers who rest content with the many-religions objection are people whose scepticism has seduced them into a fatal “repose”. If they were really bent on knowing the truth, they would be persuaded to examine “in detail” whether Christianity is like any other religion, but they just cannot be bothered. Their objection might be sufficient were the subject concerned merely some “question in philosophy”, but not “here, where everything is at stake”. In “a matter where they themselves, their eternity, their all are concerned”, they can manage no better than “a superficial reflection” (“une reflexion légère”) and, thinking they have scored a point by asking a leading question, they go off to amuse themselves. As Pascal scholars observe, Pascal regarded the many-religions objection as a rhetorical ploy, a “trap” that he had no intention of falling into. If, however, any who raised it were sincere, they would want to examine the matter “in detail”. In that case, they could get some pointers by turning to his chapter on “other religions”. As David Wetsel notes, Pascal’s treatment of the pagan religions is brisk: “As far as Pascal is concerned, the demise of the pagan religions of antiquity speaks for itself. Those pagan religions which still exist in the New World, in India, and in Africa are not even worth a second glance. They are obviously the work of superstition and ignorance and have nothing in them which might interest ‘les gens habiles’ (‘clever men’) Islam warrants more attention, being distinguished from paganism (which for Pascal presumably includes all the other non-Christian religions) by its claim to be a revealed religion. Nevertheless, Pascal concludes that the religion founded by Mohammed can on several counts be shown to be devoid of divine authority, and that therefore, as a path to the knowledge of God, it is as much a dead end as paganism. Judaism, in view of its close links to Christianity, he deals with elsewhere. the many-religions objection is taken more seriously by some later apologists of the Wager, who argue that, of the rival options, only those awarding infinite happiness affect the Wager’s dominance. In the opinion of these apologists “finite, semi-blissful promises such as Kali’s or Odin’s” therefore drop out of consideration. Also, the infinite bliss that the rival conception of God offers has to be mutually exclusive. If Christ’s promise of bliss can be attained concurrently with Jehovah‘s and Allah‘s (all three being identified as the God of Abraham), there is no conflict in the decision matrix in the case where the cost of believing in the wrong conception of God is neutral (limbo/purgatory/spiritual death), although this would be countered with an infinite cost in the case where not believing in the correct conception of God results in punishment (hell). Furthermore, ecumenical interpretations of the Wager argue that it could even be suggested that believing in a generic God, or a god by the wrong name, is acceptable so long as that conception of God has similar essential characteristics of the conception of God considered in Pascal’s Wager (perhaps the God of Aristotle). Proponents of this line of reasoning suggest that either all of the conceptions of God or gods throughout history truly boil down to just a small set of “genuine options”, or that if Pascal’s Wager can simply bring a person to believe in “generic theism” it has done its job. Pascal argues implicitly for the uniqueness of Christianity in the Wager itself, writing: “If there is a God, He is infinitely incomprehensible…Who then can blame the Christians for not being able to give reasons for their beliefs, professing as they do a religion which they cannot explain by reason?” ref
Argument from inauthentic belief
Some critics argue that Pascal’s Wager, for those who cannot believe, suggests feigning belief to gain eternal reward. This would be dishonest and immoral. In addition, it is absurd to think that God, being just and omniscient, would not see through this deceptive strategy on the part of the “believer”, thus nullifying the benefits of the Wager. Since these criticisms are concerned not with the validity of the Wager itself, but with its possible aftermath—namely that a person who has been convinced of the overwhelming odds in favor of belief might still find himself unable to sincerely believe—they are tangential to the thrust of the Wager. What such critics are objecting to is Pascal’s subsequent advice to an unbeliever who, having concluded that the only rational way to wager is in favor of God’s existence, points out, reasonably enough, that this by no means makes him a believer. This hypothetical unbeliever complains, “I am so made that I cannot believe. What would you have me do?” Pascal, far from suggesting that God can be deceived by outward show, says that God does not regard it at all: “God looks only at what is inward.” For a person who is already convinced of the odds of the Wager but cannot seem to put his heart into the belief, he offers practical advice. Explicitly addressing the question of inability to believe, Pascal argues that if the Wager is valid, the inability to believe is irrational, and therefore must be caused by feelings: “your inability to believe, because reason compels you to [believe] and yet you cannot, [comes] from your passions.” This inability, therefore, can be overcome by diminishing these irrational sentiments: “Learn from those who were bound like you. . . . Follow the way by which they began; by acting as if they believed, taking the holy water, having masses said, etc. Even this will naturally make you believe, and deaden your acuteness.—’But this is what I am afraid of.’—And why? What have you to lose?” Some other critics have objected to Pascal’s Wager on the grounds that he wrongly assumes what type of epistemic character God would likely value in his rational creatures if he existed. More specifically, Richard Carrier has objected by positing an alternative conception of God that prefers his creatures to be honest inquirers and disapproves of thoughtless or feigned belief (Richard Carrier, The End of Pascal’s Wager: Only Nontheists Go to Heaven): Suppose there is a god who is watching us and choosing which souls of the deceased to bring to heaven, and this god really does want only the morally good to populate heaven. He will probably select from only those who made a significant and responsible effort to discover the truth. . .Therefore, only such people can be sufficiently moral and trustworthy to deserve a place in heaven — unless God wishes to fill heaven with the morally lazy, irresponsible, or untrustworthy. ref
- DECISION MAKING ENVIRONMENT Introduction History Meaning Definition Explanation Example Concept Objective
- INTRODUCTION DECISION MAKING PROCESS 1. Recognizing & defining the situation 2. Identifying the alternatives 3. Evaluating the alternatives 4. Apply the model 5. Selecting the best alternatives 6. Conduct a sensitivity of the solution 7. Implementing the chosen alternatives 8. Following up & evaluating the result
- TYPE OF DECISION MAKING ENVIRONMENT Decision making under certainty Decision making under uncertainty Decision making under risk
- DECISION MAKING UNDER CERTANITY Assume that complete knowledge is available ( deterministic environment ) Example U.S. treasury bill investment Typical for structured problem with short time horizons Some time DSS approach is needed for certainty situation
- DECISION MAKING UNDER CERTANITY .2 there is only one type of event that can take place. It is very difficult to find complete certainty in most of the business decisions. in many routine type of decisions, almost complete certainty can be noticed. In uncertainty the decision are of very little significance to the success of business.
- DECISION MAKING UNDER CERTANITY .3 The decision maker is not in a position, even to assign the probabilities of happening of the events. In the environment of uncertainty, more than one type of event can take place and the decision maker is completely in dark regarding the event that is likely to take place. Such situations generally arise in cases where happening of the event is determined by external factors. For example, demand for the product, moves of competitors, etc. are the factors that involve uncertainty.
- MAXIMAX CRITERION OR CRITERION OF OPTIMISM This criterion provides the decision maker with optimistic criterion. The working method is summarizing as follow. Locate the maximum payoff value corresponding to each alternative, then select an alternative with maximum payoff value.
- MAXIMIN CRITERION OR CRITERION OF PESSIMISM This criterion provides the decision maker with pessimistic criterion. The working method is summarizing as follow. Locate the minimum payoff value corresponding to each alternative, then select an alternative with maximum payoff value
- MINIMAX CRITERION OR MINIMUM REGRET CRITERION This criterion is also known as opportunity loss decision criterion or minimum regret criterion. The working method is summarizing as follow. Determine the amount of regret corresponding to each state of nature. Regret for jth event corresponding to ith alternative is given by Ith regret = (maximum payoff- Ith payoff) for the Jth event Determine the maximum regret amount for each alternative. Choose the alternative which corresponding to the minimum of the maximum regrets.
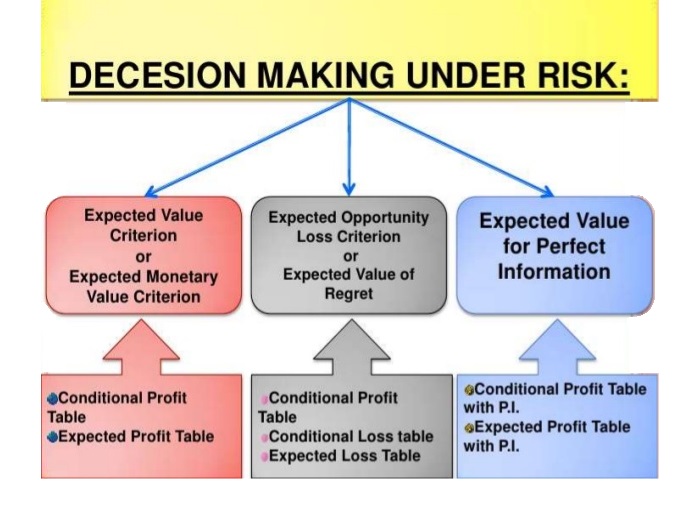
- DECISION MAKING UNDER RISK Here more then one state of nature exists and the decision maker has sufficient information to assign probabilities to each of this states. These probabilities could be obtained from the past records and simply the subjective judgment of the decision maker. Under condition of risk, knowing the probability distribution of the state of nature, the best decision is to select the course of action which has the largest expected pay off value.
- DECISION MAKING UNDER RISK .2 Under the condition of risk, there are more than one possible events that can take place. The decision maker has adequate information to assign probability to the happening or non- happening of each possible event. Such information is generally based on the past experience. Every decision in a modern business enterprise is based on interplay of a number of factors. New tools of analysis of such decision making situations are being developed. These tools include risk analysis, decision trees and preference theory.
- EXPECTED OPPORTUNITY LOSS CRITERION EOL represent the amount by which maximum possible profit will be reduced under various possible stock actions. The course of action that minimizes these losses of reductions is the optimal decision alternative. The procedure the calculate expected opportunity losses is as follow. Prepare the conditional profit table for each decision event combination and write associated probabilities. Foe each event determine the conditional opportunity loss (COL) by subtracting the payoff from the maximum payoff for that event. Calculate the expected opportunity loss for each decision alternative by multiplying the COL’s by the associated probabilities and then adding the value. Select the alternative that yields the lowest EOL.
- DECISION TREE Instances describable by attribute-value pairs e.g Humidity: High, Normal Target function is discrete valued e.g Play tennis; Yes, No Disjunctive hypothesis may be required e.g Outlook=Sunny Wind=Weak Possibly noisy training data Missing attribute values Application Examples: Medical diagnosis Credit risk analysis Object classification for robot manipulator (Tan 1993)
- TOP-DOWN INDUCTION OF DECISION TREES ID3 1. A the “best” decision attribute for next node 2. Assign A as decision attribute for node 3. For each value of A create new descendant 4. Sort training examples to leaf node according to the attribute value of the branch 5. If all training examples are perfectly classified (same value of target attribute) stop, else iterate over new leaf nodes.
- BAYESIAN ANALYSIS ( | ) ( ) ( | ) ( ) j j j p x P P x p x Suppose the priors P(wj) and conditional densities p(x|wj) are known,
- UTILITY THEORY Step for determine the utility for money : 1. Develop a payoff table using monetary values 2. Identify the best and worst payoff value 3. For every other monetary value in the original payoff table 4. Convert the payoff table from monetary value to calculate utility value. 5. Apply the expected utility criterion to the utility table and select the decision alternative with the best expected utility. Ref